TS
hpykurnia
Penjumlahan Bilangan Biner
Hai Gan/ Sist ane mau ngelanjutin pembahasan sebelumnya tentang konversi bilangan biner ke desimal maupun sebaliknya, tapi kalo ane lihat ada gambar tabel yang nggak kebaca ya di pembahasan sebelumnya https://www.kaskus.co.id/post/5f13c6...c7238b75b0561  ane minta maaf nih ane kasih lagi tabel gambarnya biar lebih jelas
ane minta maaf nih ane kasih lagi tabel gambarnya biar lebih jelas 
Skema Bilangan Biner
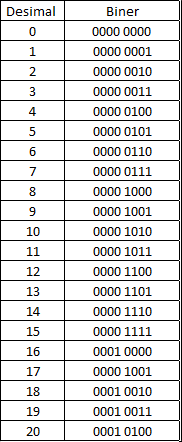
Fiuuhh akhirnya lega juga, ini tabelnya ya Gan, buat yang masih pada penasaran konversi bilangan biner bisa dilihat disini https://www.kaskus.co.id/post/5f13c6...3c7238b75b0561
Kali ini ane mau ngebahas penjumlahan bilangan biner
Nih ane kasih basic penjumlahan dulu ya :
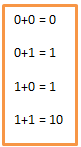
Kita ambil contoh aja 777+135=912 (Desimal)
kita konversi dulu 777 jadi biner yaitu 001100001001 dan 135 yaitu 10000111
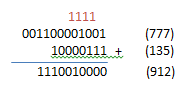
Ane jelasin dari arah kanan ya Gan, ini sama kaya penjumlahan bersusun biasa.
dari arah kanan ke kiri.
1+1=10, nah angka nol kita tulis di bawah dan angka 1 nya kita simpa di atas yang merah itu ya.
Terus geser ke baris 2, 1 merah+0=1+1 = 10, nah kita simpan lagi angka satunya ke samping atas, yang merah ya dan angka nolnya kita taruh di bawah.
Lanjut ke baris 3 , 1 merah+0=1+1 =10, kita simpan angka 1 jadi merah di samping atas lagi dan angka nol kita tulis di bawah.
Lanjut ke baris 4, 1 merah+1 = 10, nah angka 1 nya kita simpan lagi di samping atas dan angka nolnya kita tambah dengan angka nol bawah jadi 0+0=0.
Kita ke baris 5, 1 merah + 0=1+0=1.
Baris ke 6, 0+0=0.
Baris ke 7, 0+0=0.
Baris ke 8, 0+1=1.
Terus selanjutnya ada dua angka 1 di turunin aja Gan.
Nah jadilah angka 912 = 1110010000.
Begitu penjelasan dari ane, bingung nggak Gan
Semoga nggak bingung ya nah untuk berikutnya ane mau kasih penjelasan lagi yaitu pengurangan bilangan biner, perkalian dan pembagian.
nah untuk berikutnya ane mau kasih penjelasan lagi yaitu pengurangan bilangan biner, perkalian dan pembagian.
Ternyata bilangan biner nggak cuma konversi aja Gan hehehe ternyata pembahasannya banyak cakupannya. Ane pikir ane udah jago banget, ternyata masih cupu Ditunggu lagi pembahasan biner berikutnya ya dengan pembahasan pengurangan
Ditunggu lagi pembahasan biner berikutnya ya dengan pembahasan pengurangan 
semoga bermanfaat dan bisa dipahami ya Gan/Sist.
Kurang lebihnya mohon maaf
Terima kasih
 ane minta maaf nih ane kasih lagi tabel gambarnya biar lebih jelas
ane minta maaf nih ane kasih lagi tabel gambarnya biar lebih jelas 
Skema Bilangan Biner

Fiuuhh akhirnya lega juga, ini tabelnya ya Gan, buat yang masih pada penasaran konversi bilangan biner bisa dilihat disini https://www.kaskus.co.id/post/5f13c6...3c7238b75b0561
Kali ini ane mau ngebahas penjumlahan bilangan biner
Nih ane kasih basic penjumlahan dulu ya :
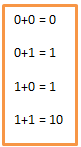
Kita ambil contoh aja 777+135=912 (Desimal)
kita konversi dulu 777 jadi biner yaitu 001100001001 dan 135 yaitu 10000111
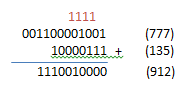
Ane jelasin dari arah kanan ya Gan, ini sama kaya penjumlahan bersusun biasa.
dari arah kanan ke kiri.
1+1=10, nah angka nol kita tulis di bawah dan angka 1 nya kita simpa di atas yang merah itu ya.
Terus geser ke baris 2, 1 merah+0=1+1 = 10, nah kita simpan lagi angka satunya ke samping atas, yang merah ya dan angka nolnya kita taruh di bawah.
Lanjut ke baris 3 , 1 merah+0=1+1 =10, kita simpan angka 1 jadi merah di samping atas lagi dan angka nol kita tulis di bawah.
Lanjut ke baris 4, 1 merah+1 = 10, nah angka 1 nya kita simpan lagi di samping atas dan angka nolnya kita tambah dengan angka nol bawah jadi 0+0=0.
Kita ke baris 5, 1 merah + 0=1+0=1.
Baris ke 6, 0+0=0.
Baris ke 7, 0+0=0.
Baris ke 8, 0+1=1.
Terus selanjutnya ada dua angka 1 di turunin aja Gan.
Nah jadilah angka 912 = 1110010000.
Begitu penjelasan dari ane, bingung nggak Gan

Semoga nggak bingung ya
 nah untuk berikutnya ane mau kasih penjelasan lagi yaitu pengurangan bilangan biner, perkalian dan pembagian.
nah untuk berikutnya ane mau kasih penjelasan lagi yaitu pengurangan bilangan biner, perkalian dan pembagian. Ternyata bilangan biner nggak cuma konversi aja Gan hehehe ternyata pembahasannya banyak cakupannya. Ane pikir ane udah jago banget, ternyata masih cupu
 Ditunggu lagi pembahasan biner berikutnya ya dengan pembahasan pengurangan
Ditunggu lagi pembahasan biner berikutnya ya dengan pembahasan pengurangan 
semoga bermanfaat dan bisa dipahami ya Gan/Sist.
Kurang lebihnya mohon maaf

Terima kasih

prahayuh memberi reputasi
1
4.6K
1
Komentar yang asik ya
Mari bergabung, dapatkan informasi dan teman baru!
Education
23.3KThread•16.3KAnggota
Tampilkan semua post
TS
hpykurnia
#1
Konversi Bilangan Desimal ke Biner dan Bilangan Biner ke Desimal
Kali ini ane lagi kangen banget sama masa-masa SMA Gan/Sist. Bukan masalah drama pertemanan atau percintaan tapi malah kangen sama bilangan yang bikin ane jatuh hati dan ane suka banget sama bilangan ini sampe kunci helm ane, ane bikin pake bilangan ini. Bilangan apakah gerangan itu ? 
Yapzzz bilangan desimal Gan
Yuk kita bahas sejarahnya dulu.
Definisi Bilangan Biner
Definisi Bilangan Biner atau dalam Bahasa Inggris “Binary” adalah sebuah jenis penulisan angka menggunakan dua simbol yaitu 0 dan 1.
Bilangan biner pertama kali digunakan dan dikenalkan di awal abad 70-an oleh Thomas Harriot. Dalam bilangan biner juga berlaku penambahan, pengurangan, perkalian, dan penambahan.
Sistem bilangan biner ini adalah sebuah dasar dari semua bilangan yang berbasis digital. Dari bilangan biner kita bisa mengkonversi ke bilangan desimal dan sebaliknya.
Sistem bilangan biner bisa juga disebut dengan bit atau Binary digit. Pengelompokan biner dalam istilah komputer selalu berjumlah 8, dengan istilah 1 Byte.
Nah sekarang kita masuk ke konversi ya Gan.
Konversi Bilangan Desimal ke Bilangan Biner
Nih ane punya tabel skema bilangan biner
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAANMAAAG5CAYAAAAUHwFRAAAgAElEQVR4Ae1d0ZHcOoycuCYBZ7JVTsVfG4Yj2BBeEOe7LweiK0oitwlSHIkDCKLcrnpvQIEEqAZa1GhFzON//vf/Jv5HDJgD7+fAI4DIfz4IPB4PH8f0qo5AiCXJpA7rfoMk036srt6TZHKOEMnkHABF9ySTIpg9pkimHtSuOYZkco4LyeQcAEX3A5Ppa/oIX/geH9OXIiCLqT/T59PKdj7ZMcgUsQ6Y4H/P6fNPPJ/zMIser/ZpTKZ6EJ7fEXgDj2ibZHoDxJ1DV6w/8LIl8SeZziHT83OKF7A/n8/l6pYFZmdMT+t2XmIMtTKJmH19hFUKV6fTAnRJR6eTKaCwBOExfccmJm+8hcgDFPvPk02D4ph1ZfrzOT0fj+n5+bXeoi22Qnccn4YvE8luW75XTGHbMHTjkmldmdKFUmL2rf+cSfcdj2844+q2xj3ZmoOz3MY/n3NcbW7nv2eiIbmQKa5OS/LKIMTkX0ny9TEnfEz0P58f6326GLeSKV0pUzsQLKyLMXBAvhQ8YWuSbQ2o6zaGIlP2fSkQAC96ErOId+zzTa7lLmVnO/NRx/AqR13INCFBYtLjkrHq50Or/EiJH6ETwYt2Uj+hTytiDG60s3zmtyzl2Ly3XmsoMmGM0gUn3mFIzCRZhB5zYIVzucjG+MjxephbWXIhU7YyRbIUV70YpLhSrbcC6emdCE4HmfD2bwYiXQWFbSv0p2ledQ3NK5leEzsj03x1grsGiZkkQ66PObDgHmO7fC5u5HilUzE040KmbBWoXKG2zjcGoHp7eJBM0VbMj2xO6apr8aQwP7sQgOv/0ydTdndSBYBkErCUgMQkfsQslt9lhIXQP35fygOQX+mmLjKJWwquTAL92KyTqX0BkrEX8Ypx37wtl+PjXK77ec7KJG7hEjkSLitwWb+4KsQgrLcCiYTxODxQCOM3gxNvFyWB1luLj/CgI+qE7TRPfWGolSmLD96SBVwkZpIMUh/GyLjHmIMuxVMfe22LxmTSnu797I1BpvvhbnFGJJMFqgdskkwHwLp4V5LJOUAkk3MAFN2TTIpg9pgimXpQu+aYRKZZqHzB5PH1wQexyV69Yl5s5AVrQPhd6UJS8t89EJgvMCSTXzBJJj/stT2TTNqIHrRHMh0E7MLdSSbn4JBMzgFQdE8yKYLZY4pk6kHtmmNIJue4+JApvtoTnkjhKzwBDAudBNnCR8um9G/THptM8eXW9bF1em3PBisTqx5kml9QXcFCOZwgtlF+RyeBQ7sov+MD7aAsfVu2BybT8pJkeml23soRX1S1hEzX9vlkCrgBTvMFKa5OFjqJl4WPlk3p3649Lplm8sQkCAAty/xoq9PpZMrIE3CDRLTQydy18NGyKf0btocl07wvKns9fyFTWqkMQdM0TTKdTGbN4AlbNyLTcr9PMokIy2brKm6hu5p/OR/F9o3IxJVpV15YEKZlU06q1ddCJ/0btocl07KFnd+ZjucG3FaFwVkCW+jkDC18tGxK/3btccm0bnlODxyKBxJ2oGlaDgE4+x8+OkY5zAPbKL+jk+eHdlF+xwfaQVn6tmwPTKZ4VY2vwsPjXkvElG17kCmvvYCrezi5cJWPmGrpJGgWPlo2pX+b9thkssHkVKs+ZDr1FP8ZZySTc6hJJucAKLonmRTB7DFFMvWgds0xJJNzXEgm5wAouk9kmoX0xTN+AeUncWEOHMoBbltXvDwdNBUCxX/3QGAmHcnkF0ySyQ97bc8kkzaiB+2RTAcBu3B3ksk5OCSTcwAU3ZNMimD2mCKZelC75hiSyTku55KpVSfBQifBNfSRvbAr/Z7THp5M8cfTRtvHFMN7JpnwBVCUw1ywjfI7uniO8RPtovy+j/hennyXMHo+53NgMi0APj+/ps9n/EX1c0DT9HIemQJe8DJwdiW30EmUbHyki+nHx/QsKi3JOdi2ByZTBGbMTYFx9qeRKSNP8A7JbaGLJxg/jXz8+fqa/gQfhf3o+LxPkuk8rKueSKYaEXYSHRElmRCNXpkr0y7kimTbmbC94+Skeu20xqGPoh8qz5G5Mp2D86YXrkxcmTaT43wFV6Z9mMNKFAZkV3ILnZyVsY/sfKTvc9pcmc7BedPLaSuT0eNvfMSNcu2EUY9y6IttlF/pkh+SKUHRIYQrXbk9YLS/N51JJpv6DhiHV3/nafXt1a2pQzJ1cOhmQ84l083Au9jp3OA272KIHpwOyXQQsAt3J5mcg0MyOQdA0T3JpAhmjymSqQe1a45JZJqFyhd6Hi8fchATYrKZA9y27nelC0Hhv3sgMBOMZPILJsnkh722Z5JJG9GD9kimg4BduDvJ5Bwcksk5AIruSSZFMHtMkUw9qF1zDMnkHBdfMlnUZGjZlGC3+rZ0q53qK0Q7xslpKLWHJlPcsjyfxOMxpR8+UwLnDDOeZMIXSlEO541tlN/RSTzRLsqvfCx24rt8+fuAaAdl6duiPS6ZwlUJfm19IVYOrAVg2jb9yBSSccSaEGH3yHMKuD2Lug+tc9KOXGlvXDLJc5mXfEgOqb9o241MxS0SJKKFTuLf6yNsxdqq+9CyKf0btO9DJv6m7bH0aCWehU7OrtcH2pE2ZBuLxuA4I/kmZFq+dI62lynElCtTzOydK2PsHj4leWSbZEK09snzF034/rRv1DV6kUwxDiRTRMLtc2QiBdDcyCSv2tlVHRI7TFJFJ1Ok1wfYyeYVjrdswjgjceDbvPXvCYOuSDGefmSyefyNj6NRjueLn6hHOfTBNso4Pif5osG+KGfjjBrjkml+4FDZCjDYH5s8yTRuTYiVDcXKFI6H1Snmxbl/KhmXTEZXl7PN+pLp7LO9tz+SyTm+JJNzABTdk0yKYPaYIpl6ULvmGJLJOS4kk3MAFN0nMs1C+uIWv8Dxk7gwBw7lALetK16eDpoKgeK/eyAwk45k8gsmyeSHvbZnkkkb0YP2SKaDgF24O8nkHBySyTkAiu5JJkUwe0yRTD2oXXMMyeQcFx8y/Z1+//wx/fgR/vs1/ZdhYKHLHEzT1OtjtfP39/SzmPcOnZyGcntoMsXty/NJOP9sfW9cPMj0368f049fC4VQDueAbZTf0Uls0C7Kr3wsdv6bflUvAvPohk7OQr89MJm+pg94Y/zsN4S1QnE+mUIy/px+/13PILvKW+gkUr0+punv75/zavrz169iZWrp5Ays2gOTKYdkXqWAXLn2uq3TyZSRJ+ACyW2hk9D3+gg3h//9N83XgMJGWyenYNW+CZmW1+65bX1HmhSJOA6Z0tkV55A0YfkqVi3Qmopjkwn3NA22jylGlSvTTjJHwMJnizAtHdowkMcmEwDCunkARksskm1nMveOk3PRsFPYACctHXSzEG9DpmULM+vmvU4SIE/onCWfhU7OqNcH2MnmDMeL8xE64+a4ZApbluHWjivT/kzBx9EoBwvYRvkdnZwZ2kX5lY9kh2RKUCgJWKA9bBMYb1UKQJz+nWlGP6wOW3+0tdDJkPf6WO2QTBJQtgMCPmQi9hYIjHubZ4GGg02SyQF0I5ckkxGwe82STHuRun4/ksk5RiSTcwAU3ScyzQJrQMzfYYgF6z505wC3rSteng6aCkHjv3sgMBOQZPILJsnkh722Z5JJG9GD9kimg4BduDvJ5Bwcksk5AIruSSZFMHtMkUw9qF1zDMnkHBcfMvXWYOgdJ0Fu2Vn7Vl8Zao1r6aR/m/YtyDRvWQ8/Zf/5xwYlQ6seZMKXS1EOp4ltlN/RSfjQLsrf/eK7e3mxF+yL8qu5fdu1lcYnU9gg+PyYPp4k075UCYl61RoQrToPvfPeh4pGr8HJtLw5/vHFX1vfnQzF7RMkqYVOTqzlo1XnoTWupZP+DdtDk2newzTvaSKZdudIK/EsdHJiLR/YV/aT7b2FYNCmsTwumbLfMyWZdudJb1L2jpMTa9nBvrKfbJNMiNY7cry9izZIpojEy8/epOwdJyfUsoN9ZT/ZJpkQrXdk/EVt8VLmYLXzwq3Buf/gO1JwnCWphU6eXcsH9M3mFY63xrV0YNNYHPc2LwOGK1MGx4sGPlZGOQzDNsrv6OR00C7KWb+CTP1zy+waNkgmQ3D3mD5/ZQqzClfyq9aAWFGrkKl/3nsi8X6fm5DpfSC8LPiQyets7+2XZHKOL8nkHABF9ySTIpg9pkimHtSuOYZkco4LyeQcAEX3iUyzwBoQrAHBHHgvB7htXfHydNAUV6aDgF24e1qZLjzHW0+NZLpPeEkm51iSTM4BUHRPMimC2WOKZOpB7ZpjSCbnuJBMzgFQdE8yKYLZY8qHTK16CRY6iUzLx9q3+jpR7zjp36Y9MJmWl1vnE4iPc+HHz2zg0rfqQSZ8uRTlcHbYRvkdnUQN7aL83S++O7i/BsQytj7u266tNDyZBuRPFtHzydTarmChy073xVaK3hoQrXHSv12bZLLDdpfl08lU3D4BgSx0EoWWj94aEK1x0r9he3gyzScw3+bxZzh35UkrmS10clItH9hX9pNtuVkwji36RYX958BkysHhD0TneGy2imS71sqU5i3nKdskU4LKQFi2so/2HYq3eUBmzApJHtkmmRAtZXmuVjTerd7pZJJJmCWpSGwVnYxzywf0zXyH473jwKaxOOxt3tdHTpy5RPJgxVRCbM8nk83jb3zEjXItf1GPcta3IFN73mlsZVzSGQvDkmkKZZHj35fC54BECrH1IFN/LYWwOvTUjpBZ3LKz9q2Sonec9G/THpdMNnicbtWHTKef5j/hkGRyDjPJ5BwARfckkyKYPaZIph7UrjmGZHKOC8nkHABF94lMs4Bf6CnnDziIB/HYkwOsAaF4eTpoiivTQcAu3D2tTBee462nRjLdJ7wkk3MsSSbnACi6J5kUwewxRTL1oHbNMSSTc1x8yNTa/m2hkyC3fKx9q29AtHQ7bMppKLdJJmVAj5rzIBO+D4dymDu2UX5HJzFBuyh/94uvDeXb1hd9XYd2UP62aS8NT6ZlH1P89cD85Vd7+N73cD6ZQjL+nH7/XeeerQAWOolRy0d7+/nf3z+nHz9+TD9//Zp+/kCitW3KGVi1hybTTKRBX3CNAT2dTBl5wiwgES108UTjZ8vHi+3nf//7b5qvAdKGbOM5Rb8nfA5MprAZcLyVSMaUZAIyIzgFQUApdbJNMgFYe8R1M+DzGW/xHtNjtG22HlswWolnoZOxbPnAvkU/UEqdbJNMANYecd7PBCvTTK7HNBqfuDJxZdqT7rZ9ZjJ9TF/Jy5i/uH46meRVO7uqi8RW0aUArULLB/TNfMPxIBa6nTaFGe3muN+ZipoPJNPe5MBHxyiH8dhG+R2dnBfaRTnrVxAGtBUd2kEZRpmL45JpEuSRt33m0Ok4OH9lCvMOV/Ke7ee94yRWLTtr3wphkpWqbofNZMBGGJhM0zSt35Pmk3iM930phNSHTDbJ9K9bHZtMN4geyXSDIK6nQDI5x5Jkcg6AonuSSRHMHlMkUw9q1xxDMjnHhWRyDoCi+0SmWdizx519WAuBObCdA6wBoXh5OmiKK9NBwC7cPa1MF57jradGMt0nvCSTcyxJJucAKLonmRTB7DFFMvWgds0xJJNzXHzI1KqXYKGTILd8rH2rrwy9qZPTUG6TTMqAHjXnQSZ8ERTlMHdso/yOTmKCdlH+7hffs8Ot6VHbq4vj7T7HJZP8fab0uBa3ZdgBp2X5fDKFZLxbDYh27QitWL2yMy6ZKmc2/3rgYLsDTydTcfsE5LLQyTi1fPTWgHgxTk7Bqn0fMhX7m6wg07VLMgGZEdqCdKDs1YEJC/E2ZBpxVQoBJZlIJgtiv2EzVCrifqZdABZXdUhmC52cVMsH9i36gbJXByYsxFusTCPXzzt9ZbplDQigRoto0M1CvAGZxl2VQkDPJ5PN4298xI1yLWlRj3LWt0WKXl3mQL8xPJmW8shjPQ7HMHqQ6Z41IFZUW0RD4A3kwcm0rErPzz8G0Jxj0odM55zbv+ZlcDKNHy6SafwYxjMgmSISTp8kkxPwBm5JJgNQj5gkmY6gde2+JJNzfEgm5wAouk9kmoX0sij8sgSPbe/3JzbERuYAa0AoXp4OmuLKdBCwC3dPK9OF53jrqZFM9wkvyeQcS5LJOQCK7kkmRTB7TJFMPahdcwzJ5BwXksk5AIruSSZFMHtM+ZCpVdDEQreBTPU9uhP9b0yr9/DYZBJ1IEZ8R8+DTPimNsohibCN8ju6enKGfVThB9fyoinoE2V9//VZvXN0YDKFl1zlD0RD+x1UThx7PplgM2A4z2x1sNCVYP79/XP68ePH9PPXr+lnRqZz/Jcz0jkyLpnmmg+49UKQSwcfcyunkykjTzg9SGALXQXBv//9N/0Nx6U/2daYW8W/1aFxyTRN01z34REIJX7f1gotA7v/IpkSjJI8sk0yJahOERZCPabH83MacVcTyQTfmUimUzhTcZJvV1923PI7UwWo/JBFwrZs5t7zlhwn21yZcrysWmURlTFv9U5fmTBBQ3CyBIbvT2q6RgZkvkO/k/03ptajGvc70/xYHB5AzA8kxiv3dT6ZbB5/42NslJtJWZDJZm7NOSgqxyVTegDxvV2Ef2famxlhBQh/4yn/zmNTbGVjXhUynep/Y1q9h4cmU+9JX2mcx8p0pfO/01xIJudokkzOAVB0TzIpgtljimTqQe2aY0gm57iQTM4BUHSfyDQLcj8726xxwBw4lgOsAaF4eTpoiivTQcAu3D2tTBee462nRjLdJ7wkk3MsSSbnACi6J5kUwewxRTL1oHbNMSSTc1xIJucAKLonmRTB7DHlQyaLOgstmxvIVF8natlp6VYfVZsb/pUPj02mrAbEeNsvQiw9yIQvoqIc5oNtlN/R1XM2vh8I+5ne8L/4qNus+9c/Oi6ZZiIBgeRb5PpYmVg8n0wW2xxaNkvY9GtAhJ0kW3UlSv9WR4YlU7mfiTUgdiVJcRsERLDQVSalXgMibMvaqitR8W91aFgyTcVKlO+8tQJM2+7pK5MFYVo2W4DJcbKNmwVbOvRR9EOlrTwumYr9TM/p+eTmwJfpUiTb+StTmqOci2yTTAmqkwWuTLsA703Y3nGtSUmbsk0ytdAz1BW3fYa+FE2ffpuHCRrOI0tgWKXUdA2wMt+hX69/8FHYBJ2xOPRt3jc2y6rEbevfiLQkfOSNchiDbZTf0W3OpZL46BPlV/6Tj4rNpDMWxiXTWkBlPoHHYxqRSCG2569MwWtYAe5WA2JlCslkfMm4sHkfMl0YkIGnNu7KNDDoOHWSCdEYWyaZnONHMjkHQNE9yaQIZo8pkqkHtWuOSWSaBe73P7bfn3gRL5kDrAHhd6XjyuSHvbbntDJpG6a9fQiQTPtwGqEXyeQcJZLJOQCK7kkmRTB7TJFMPahdcwzJ5BwXksk5AIruSSZFMHtM+ZCpVUvBQreBTPXVn5b/1U7vuI1paB0ejkzLz21W3sUT7+p9fGlBZGvHg0z4AinK4UyxjfI7ujqC8f3A/TUgFju94+qz0Dw6EJnim+Ff0+dTkinq1p+IlvUhNBFTtnU+mXq3OfSOKwHbrtfQ8tGq89AeV87A5shAZIoAVH67ttjLtPQZYXU6nUzFLRIkooUuhg0+N+s1tPy36jy8GAeuTcVbkKksrlIhnCmM/cb/RTIltCQJZFtuFowDZT/Z3hoXxxt93pRM0/T1IW8FjRB80yzJBN+Z9pJC9pNtkmlvVparDlemvdjJbeph3Pm3eWm2kgSyjXNLgyrnsHcc2jCQb7EylWW/+J1pO1eAPKFTlogWuu2Z5L5Dv5Z/sJPN+cA4MGEh3oNMk6hMVDyQsIBOx+bpt3lGj7/xMTrKTZQKUrQfzSdbveOSARthIDIthJknDK+9p9oP2d+ZoGyyDW5qVj3ING4NiBX2Cpna56QWrqahgcjUPI9hlT5kGhauS0+cZHIOD8nkHABF9ySTIpg9pkimHtSuOYZkco4LyeQcAEX3iUyzAF/s2X6wvgHz4XgOsAaE4uXpoCmuTAcBu3D3tDJdeI63nhrJdJ/wkkzOsSSZnAOg6J5kUgSzxxTJ1IPaNceQTM5xIZmcA6DonmRSBLPHlA+ZWnUWLHQbyFRfC2r5X+1Ux+3QbUxD6/BwZNqsATFNU0unBZi2HQ8y4YuoKIdzwzbK7+jqmIU3xMNvRMF+phf+Fzv1ca919VloHh2ITLHOQ6sGRE2nCZe+rfPJ1NrmYKErMdOvAdGqD1H6tzoyEJkiBOXmwKiZppbuu9eVpNPJVNwiAYEsdBWw1WtAtOpDVPxbHSKZrJDdafdfJFOCRpJXtuVmwTiw6BcVcrMjHD9BJJlOALnlgmSC70wFSWDVRBCLfqBs6aCbhUgyWaB6wCbJRDIdSBftrq3vRS2d9jx07J1OJnnrlF3JxUqgomvglNkP/Vr+wU4xbqcOulmIXJksUD1g83wy2Tz+xsfoKDehqJACx6Kc2amMS/qWLnWyEQYiU6sGREtnA5yWVQ8yteslhNUh/P2n/BtQ/7gNtKqJ3/K/2qmO26HbmIbW4YHIpHXK17LjQ6ZrYXCX2ZBMzpEkmZwDoOieZFIEs8cUydSD2jXHkEzOcSGZnAOg6D6RaRa45//4nn9iRswwB1gDQvHydNAUV6aDgF24e1qZLjzHW0+NZLpPeEkm51iSTM4BUHRPMimC2WOKZOpB7ZpjSCbnuJBMzgFQdE8yKYLZY8qHTK06Cxa6DWQOvxbUO7cN/8qHhyPTVp2HeHw+ocdjGuGX1kMsPciEL5CiHOaDbZTf0dVzNr6DB1swUse6DueD8qu5JbPGwkBkatSACD909vyc/qxgLcT6mL6MwdMwfz6ZQqL+nH7/XWefrQ4WuhKl7RoQrVoOvXMr/VsdGYhMEYIde5bmXxEc49cDTydTRp6AKSSphS6GDT43a0C0ajn0zg38Wov3JBN/03Y7b3qTsnfc9kzEj1OLjtKfbO+9CAizls0bkmnHymWJ6EHb/+LKlCAqCJI0JdGKvjtXVDBpLd6OTF8fj+kB35+sAXzXPslUewBRqTJEMr2barXx2yvPaEQKZ3c6mfD2KEwgS1K42qvpajFcj2W+Rb9C1zs3YdeweZOVaSHYSCtSjOn5ZLJ5/I2PqlGO51n9LAgDvSo6tItyGIVtlMGiuTgQmRp1HuYHDpWfzRzgj00eZOqv5RBWh576EBt5XCFM6lnVKftPznSEgcikc8JXs+JDpquhcI/5kEzOcSSZnAOg6J5kUgSzxxTJ1IPaNceQTM5xIZmcA6DoPpFpFnAvO2XWNmAOHM8B1oBQvDwdNMWV6SBgF+6eVqYLz/HWUyOZ7hNeksk5liSTcwAU3ZNMimD2mCKZelC75hiSyTkuJJNzABTdk0yKYPaY8iFTby2F3nEbyFRfGVr7VnUt/61xG/6VDw9Hpljr4fkZN6kviMTj8wk9xtiyHmbuQSZ8ERTlMB9so/yObomQ/H98z662BaOuw/mg/G25Pu5bbysNRKZGDYjpa/qAPUzzVowBXnINoT2fTCHh7lYDolU7wpZAaH0gMsVpb+9nSj0+n8NsEDydTMXtE5DLQheDAp/qNSBatSPAr7V4QzLFFSy/DbQGstf+v0imhFVB3qQRmxblJsbQDy4CMCzf7IgKe/k+ZMI9TYPc4oXwkky170wV8hTEI5kULg87b/MGeQhBMpFMCqToNfGaTBPr5jXAFVf07IpvoWtMJfMt+hW61txgbDEOdMbiPW7zAnng1o4VXdtZg4+VUQ6jsI3yO7rN2bQSv6LD+aCc2a+My/SGjYHI1KgBMa0FVdKWgTGquYa4nn6bNydTuMr31HLoHbeRwa3Er+pa/lcf1XEb/pUPD0Qm5TO/iDkfMl3k5G82DZLJOaAkk3MAFN2TTIpg9pgimXpQu+YYksk5LiSTcwAU3ScyzUL6Al8p6Ejd/LCAODE3mjnAGhCKl6eDpkJg+O8eCMwkI5n8gkky+WGv7Zlk0kb0oD2S6SBgF+5OMjkHh2RyDoCie5JJEcweUyRTD2rXHEMyOcfFh0ytWgoWug2QW6/+HNa15r3hX/nwcGSKtR5kDYiIy7xl/fGYtvSx31U+PciEL4miHDDBNsrv6OpYx/fsalswjutwrijXfdscHYhMcQft1/T53CBL2CD4/Jg+tvQ2GL5l9XwyhUQdsQZEq85D65zeCs+hwQORKZ7X1n6m5fjH15Y+jr/W5+lkKm6fIBEtdBW4u2pAtOo8tOZd8W916DZkmm//5j1NJFMzWVqJZ6FrTabwB52P6Iq+cIEAk9biPcg076yNtfJIpmbStBLPQteaTOEPOh/RFX1JJkCyJUqyLO3vjbZS37Llr/sXb/MS6gUJkqasTgSqogJRYYdkQrgasiRLfQfuvORCYcqGQVfV6WSSJbKyRBRJqKJrwJvZF/0O6VrzFnYNm/e4zcsAkmTLlJdrnE8mm8ff+Dga5SbghwgDlirj0CfKMMpcHIhM9RWo/HsSyfQ6a8KVfMQaEOuZVci0FKXcOqfXiGj0GIhMGqd7PRseK9P1ULjHjEgm5ziSTM4BUHRPMimC2WOKZOpB7ZpjSCbnuJBMzgFQdJ/INAus88A6D8yB93KA29YVL08HTXFlOgjYhbunlenCc7z11Eim+4SXZHKOJcnkHABF9ySTIpg9pkimHtSuOYZkco4LyeQcAEX3JJMimD2mfMjUqpdgodtApvpa0NrXQrcxDa3Dw5GpXgNieR9vPpn4aPd7T4YWViZ2PMiEL4KiHE4Q2yi/o6sDF98P1KkBsfho2azPQvPoQGRq1YBYyDQIf7L4nU+m1nYFC112unPj7++f048fP6afv35NP3/kZLLQlTOwOTIQmSIAtbfCSaaIzsvP4vYJCGShq0xIvQZEqz5Exb/VoVuRaT6Z+TaPP8O5mTAWhGnZ3JxIYMDvYmVK3S10ybiNcBMy5eDwB6JzPLJWkaTnr0xpPsVcksaGaGDeQgjzv4wAAArvSURBVLwlmaZp+X41wneoEIBT/xUJTDJp4X9PMs3Visa41TudTLesAQF0KC4WoDMWb0Gmr4+cOHOJ5AGKqYTYnk8mm8ff+Bgd5Wb+thLfQteczPvKgcjUqAERyiLHvy+Fz0GI5EWmdr2EcNu3VUuhV7eRqBaEadncmIbW4YHIpHXK17LjsTJdC4H7zIZkco4lyeQcAEX3JJMimD2mSKYe1K45hmRyjgvJ5BwARfeJTLOAX+Ip5w81iAfx2JMDrAGheHk6aIor00HALtw9rUwXnuOtp0Yy3Se8JJNzLEkm5wAouieZFMHsMUUy9aB2zTEkk3NcSCbnACi6J5kUwewx5UMmwzoPu17nsfDfstkTmeNjhiNTvQbEcuJRN5/UI3/59Tg054zwIBO+iIpyOGNso/xKt6AV393Lt6JLJNEuyq98YF+UX42T/q3aA5GpVQNimmYiDfSCawzo+WSC/UthEtlK0qsLZrbrOsRzXT57ffSOy71btgYiU4ShVgMiEG2MlSieRfw8nUwZecIsIEl7dUdqMPT66B0XgT7h8x5kWjcDPp+P77/Sj7DN1mM/U29StsZhohb9UClXwqBTIHPhE2wK95bNe5Bp3s8EK9NMrsc0Ap/usjKlJC0SO2kWodBD4lvohHvL5o3I9DF9JaRqt4JJeSmBZCKZHBOyQpSi5kOlj+OMW65PJxPeVoWJZasBJPYhHZxhZg+OJ7HXR++45NhcuMfKNAnyyNs+cxj7HZxPpv7H3/g4GuXs7F+SycY/zgflbG7GjYHI1KgBEUBavyfNJ/QY4/tSmLYHmWxqQKyZuoNMNv7DyrVVu8KYRav5gch0DiBne/Eh09ln+W/4I5mc40wyOQdA0T3JpAhmjymSqQe1a44hmZzjQjI5B0DRfSLTLOzZ484+329ZEAtiIXOANSAUL08HTXFlOgjYhbunlenCc7z11Eim+4SXZHKOJcnkHABF9ySTIpg9pkimHtSuOYZkco4LyeQcAEX3JJMimD2mfMi0vMs4B/+Bb9uHM7DQbSAzvwKm5X/1UbW54V/58HBkinUenp9/vqGQv8+UHlfKQH0PuYrkQab5x+DWzV4oB0ywjfI7ujrW8V3LPEboE+VX/hcfdZt1//pHByLTAtTz82v6fD6mjEwVXGQgKl0uceh8MgUc5UbKmNAWuhLmdEH8+Jie2crY63+tAfJ4TM/CZunf6shAZIoQiO0W8TB+FvubUHkt+XQyFbdBkMAWugrcf76+pvm+QvqT7fmHvlfit3Th5nTLZsW/1aFbkmmUVSkE9V8kU0pmSRDZPkCmTZtJYS/ckEzhSsv9TJup05uwveM2JxL3oMVbzEqbZGqhp6Fr3+aNVj+PKxPJpMGKThstMo21KgUATicTXu3DBLIVB74/qekaYc58h369/sFHYRN0xuKtbvOWp0RwpTMGT8P8+WSyefyN31NRbmJUSXwci3Kwg22UMx8Vm5nesDEQmZZVZ55w+jsSPiJf9K8emRti2WXag0zLChALdsqLD+KspduAppr4vf5XH1WbG/6VDw9EJuUzv4g5HzJd5ORvNg2SyTmgJJNzABTdk0yKYPaYIpl6ULvmGJLJOS4kk3MAFN0nMs0CfLFnO35B5ydz4UAOsAaE4uXpoKmQqPx3DwTmiw7J5BdMkskPe23PJJM2ogftkUwHAbtwd5LJOTgkk3MAFN2TTIpg9pgimXpQu+YYksk5Lj5kMqzzsOt1nl7/a7CqPlo2zwnycGRKW56xBkTAStSBGOUdPQ8y4UuiKC8wPqZHR32IJV3je3Xynb48mdEnyq/8t3ygHZRzz7atgcgUX2St1YAIOlnXANq2GL5l/Xwy1bCKyd+rO1KDwcJHy+Zb4Tk0eCAyxfOq7Gcqln0Bbhx6wc/TydTCqld3pAaDhY+WzRNjfg8yxb0uc6WbCtlOBPSoq7uQKZ13kdhJswiFHi58LR2akf1kW24yxLGG8m3IFDCa75XDK1HPz6X6jSFwWqZJJpJJK5c67NRWnhCQ7yIqy0MKfmeqgtu6ivfq0FFhA5Vym3zQkUwCoTObJZnKIiplnzNneMTX6SsTJm+YaJb8kNiHdHDGmT04nkQLHy2bybG5cI/bvPmxeHwiFRPke6UyR/ENB+eTqV1LAR8roxxOEdsoZ6f/kkxtO2gX5Vc+sC/K2TjjxkBkClef8lX4+PekGUDQx+PG+L1t3oNMNjUgVih2kKnff8sH5gdcWN+O0H4DA5Fp/0mN1NOHTCMhNM5cSSbnWJFMzgFQdE8yKYLZY4pk6kHtmmNIJue4kEzOAVB0n8g0C/AFnu3yYQcxISYvc4Db1hUvTwdNheDw3z0QmIlGMvkFk2Tyw17bM8mkjehBeyTTQcAu3J1kcg4OyeQcAEX3JJMimD2mSKYe1K45hmRyjosPmZYXgefgZ792HsDo1a1A7nqdyNDHLv82QR+OTPtqQIyx/SKE1INM+CIoymE+2Eb5lW5Jz/h+XPvdOLSL8vs+9vlf5qr//4HItAD1/KzUgJjfGgcCybfI9XFTs3g+mQKOgFV2Je/VedeAOOJfLXSFoYHIFOde7lUq9zOJpIhDL/h5Opky8gRAAKteXbg5/PpadjcXNgTohX6n/xc+dvsX09Fs3oJMS5kvvLUIAeJ+pmqi9CZzaxw6KvqhMu41k7FaV8piLBANzRT9QNnSQTcL8R5kivf66XWo5/R8kkzVhCmSDRK2V4eOChuoJJkEGt7N8javnBFXphKT9UiR7CTTJlYHFbdZmbLz5gOIDI68AeQJioxcvTrwkNmD40k09vHSf5qIunBDMoVgPSZuW9/OFXwcjXIYgW2UX+mStx3JjHZRVvGxw3+aq7IwEJkWkswTTt+NVtLMAH5vDxiFSCGW4XzO/4dY4sOAMJNe3XoWu5LZ0Mcu/zaID0QmGwC8rfqQyfus7+mfZHKOK8nkHABF9ySTIpg9pkimHtSuOYZkco4LyeQcAEX3iUyzAF/s2f5+oEEsiMXuHOC2dcXL00FTIUj8dw8EZsKRTH7BJJn8sNf2TDJpI3rQHsl0ELALdyeZnINDMjkHQNE9yaQIZo8pkqkHtWuOIZmc4+JDpt4aDK1xK5C7XufptdMa19KdE+ShyBTrP8yTlpv/xPt5H1/nAPiuFw8y4culKIdzwTbKr3QLDvGdO/m+X44S2kX5u1fdDvZFed/cvq1bSeOQKZAFfvh5IVYM2gJ+esFV1oSwQk/B7vlkClhdtQZEq5ZD77wVgrTTxDhkkic0r0RrUhT7l5Ylf4TV6XQyFbdhkKS9uhf1GbLQtXy07LTGtXSZc9vGuGQCApUFVRYypZXKFsO3rN+FTAmEIrGTZhEKPZAZu8p+sr23EAzaNJYHJVNOlpJMy70/yVTJnt6kbI1DN0U/VMqdvUFHMgmEzm3OXz7l9ydox6qkJFMlLkWyQzL36tBNYQOVJJNAw7cpiTTPBm75ltnxO9N2lIA8oVOW/L068JbZg+NJbPlIncS8wvHWuJYObBqLA93mLQR5ZCtQRCeACaW9CnLFftf7PP070xuPv/FxNMoZqi/J1H78nmxV7KBPlMMYbKOc7J0gjEOmmSCVrQDxkd0MftTDo98TQHzHhQeZ+us8LBetOWmKgv8rChUSlPj02mmNa+nKGVgcGYdMFmd/AZs+ZLrAid9wCiSTc1BJJucAKLonmRTB7DFFMvWgds0xJJNzXEgm5wAouk9kmgXWgJiLQhKL+CCHn0dz4f8BxAwLnPM8M58AAAAASUVORK5CYII=[/img]
Ada yang bertanya tanya gimana caranya ? Nih ane punya cara gampang banget Gan/Sist.
Konversi Bilangan Desimal ke Bilangan Biner
Misal ane ambil contoh bilangan desimal 17 itu bilangan binernya 10001 atau kalau mau di panjangin jadi 8 Byte 000010001. Cara penulisan binernya diurutkan dari hasil bagi paling bawah yaitu angka 1 dari hasil bagi 2/2 terus ke sisa paling bawah dan berurutan ke sisa paling atas.

Konversi Bilangan Biner ke Desimal
Misal ane ambil contoh bilangan 12

Nih kita kasih pangkat nol dari angka paling belakang ke depan berurutan. Dari gambar diatas udah jelas kan Gan/Sist yang ada hasilnya di jumlahkan aja
4+8 =12.
Sekian pembahasan bilangan biner dari ane, Agan Sista bisa bisa coba-coba sendiri buat latihan Untuk pembahasan selanjutnya di tunggu thread berikutnya.
Untuk pembahasan selanjutnya di tunggu thread berikutnya.
Semoga bermanfaat ya


Yapzzz bilangan desimal Gan

Yuk kita bahas sejarahnya dulu.
Definisi Bilangan Biner
Definisi Bilangan Biner atau dalam Bahasa Inggris “Binary” adalah sebuah jenis penulisan angka menggunakan dua simbol yaitu 0 dan 1.
Bilangan biner pertama kali digunakan dan dikenalkan di awal abad 70-an oleh Thomas Harriot. Dalam bilangan biner juga berlaku penambahan, pengurangan, perkalian, dan penambahan.
Sistem bilangan biner ini adalah sebuah dasar dari semua bilangan yang berbasis digital. Dari bilangan biner kita bisa mengkonversi ke bilangan desimal dan sebaliknya.
Sistem bilangan biner bisa juga disebut dengan bit atau Binary digit. Pengelompokan biner dalam istilah komputer selalu berjumlah 8, dengan istilah 1 Byte.
Nah sekarang kita masuk ke konversi ya Gan.
Konversi Bilangan Desimal ke Bilangan Biner
Nih ane punya tabel skema bilangan biner
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAANMAAAG5CAYAAAAUHwFRAAAgAElEQVR4Ae1d0ZHcOoycuCYBZ7JVTsVfG4Yj2BBeEOe7LweiK0oitwlSHIkDCKLcrnpvQIEEqAZa1GhFzON//vf/Jv5HDJgD7+fAI4DIfz4IPB4PH8f0qo5AiCXJpA7rfoMk036srt6TZHKOEMnkHABF9ySTIpg9pkimHtSuOYZkco4LyeQcAEX3A5Ppa/oIX/geH9OXIiCLqT/T59PKdj7ZMcgUsQ6Y4H/P6fNPPJ/zMIser/ZpTKZ6EJ7fEXgDj2ibZHoDxJ1DV6w/8LIl8SeZziHT83OKF7A/n8/l6pYFZmdMT+t2XmIMtTKJmH19hFUKV6fTAnRJR6eTKaCwBOExfccmJm+8hcgDFPvPk02D4ph1ZfrzOT0fj+n5+bXeoi22Qnccn4YvE8luW75XTGHbMHTjkmldmdKFUmL2rf+cSfcdj2844+q2xj3ZmoOz3MY/n3NcbW7nv2eiIbmQKa5OS/LKIMTkX0ny9TEnfEz0P58f6326GLeSKV0pUzsQLKyLMXBAvhQ8YWuSbQ2o6zaGIlP2fSkQAC96ErOId+zzTa7lLmVnO/NRx/AqR13INCFBYtLjkrHq50Or/EiJH6ETwYt2Uj+hTytiDG60s3zmtyzl2Ly3XmsoMmGM0gUn3mFIzCRZhB5zYIVzucjG+MjxephbWXIhU7YyRbIUV70YpLhSrbcC6emdCE4HmfD2bwYiXQWFbSv0p2ledQ3NK5leEzsj03x1grsGiZkkQ66PObDgHmO7fC5u5HilUzE040KmbBWoXKG2zjcGoHp7eJBM0VbMj2xO6apr8aQwP7sQgOv/0ydTdndSBYBkErCUgMQkfsQslt9lhIXQP35fygOQX+mmLjKJWwquTAL92KyTqX0BkrEX8Ypx37wtl+PjXK77ec7KJG7hEjkSLitwWb+4KsQgrLcCiYTxODxQCOM3gxNvFyWB1luLj/CgI+qE7TRPfWGolSmLD96SBVwkZpIMUh/GyLjHmIMuxVMfe22LxmTSnu797I1BpvvhbnFGJJMFqgdskkwHwLp4V5LJOUAkk3MAFN2TTIpg9pgimXpQu+aYRKZZqHzB5PH1wQexyV69Yl5s5AVrQPhd6UJS8t89EJgvMCSTXzBJJj/stT2TTNqIHrRHMh0E7MLdSSbn4JBMzgFQdE8yKYLZY4pk6kHtmmNIJue4+JApvtoTnkjhKzwBDAudBNnCR8um9G/THptM8eXW9bF1em3PBisTqx5kml9QXcFCOZwgtlF+RyeBQ7sov+MD7aAsfVu2BybT8pJkeml23soRX1S1hEzX9vlkCrgBTvMFKa5OFjqJl4WPlk3p3649Lplm8sQkCAAty/xoq9PpZMrIE3CDRLTQydy18NGyKf0btocl07wvKns9fyFTWqkMQdM0TTKdTGbN4AlbNyLTcr9PMokIy2brKm6hu5p/OR/F9o3IxJVpV15YEKZlU06q1ddCJ/0btocl07KFnd+ZjucG3FaFwVkCW+jkDC18tGxK/3btccm0bnlODxyKBxJ2oGlaDgE4+x8+OkY5zAPbKL+jk+eHdlF+xwfaQVn6tmwPTKZ4VY2vwsPjXkvElG17kCmvvYCrezi5cJWPmGrpJGgWPlo2pX+b9thkssHkVKs+ZDr1FP8ZZySTc6hJJucAKLonmRTB7DFFMvWgds0xJJNzXEgm5wAouk9kmoX0xTN+AeUncWEOHMoBbltXvDwdNBUCxX/3QGAmHcnkF0ySyQ97bc8kkzaiB+2RTAcBu3B3ksk5OCSTcwAU3ZNMimD2mCKZelC75hiSyTku55KpVSfBQifBNfSRvbAr/Z7THp5M8cfTRtvHFMN7JpnwBVCUw1ywjfI7uniO8RPtovy+j/hennyXMHo+53NgMi0APj+/ps9n/EX1c0DT9HIemQJe8DJwdiW30EmUbHyki+nHx/QsKi3JOdi2ByZTBGbMTYFx9qeRKSNP8A7JbaGLJxg/jXz8+fqa/gQfhf3o+LxPkuk8rKueSKYaEXYSHRElmRCNXpkr0y7kimTbmbC94+Skeu20xqGPoh8qz5G5Mp2D86YXrkxcmTaT43wFV6Z9mMNKFAZkV3ILnZyVsY/sfKTvc9pcmc7BedPLaSuT0eNvfMSNcu2EUY9y6IttlF/pkh+SKUHRIYQrXbk9YLS/N51JJpv6DhiHV3/nafXt1a2pQzJ1cOhmQ84l083Au9jp3OA272KIHpwOyXQQsAt3J5mcg0MyOQdA0T3JpAhmjymSqQe1a45JZJqFyhd6Hi8fchATYrKZA9y27nelC0Hhv3sgMBOMZPILJsnkh722Z5JJG9GD9kimg4BduDvJ5Bwcksk5AIruSSZFMHtMkUw9qF1zDMnkHBdfMlnUZGjZlGC3+rZ0q53qK0Q7xslpKLWHJlPcsjyfxOMxpR8+UwLnDDOeZMIXSlEO541tlN/RSTzRLsqvfCx24rt8+fuAaAdl6duiPS6ZwlUJfm19IVYOrAVg2jb9yBSSccSaEGH3yHMKuD2Lug+tc9KOXGlvXDLJc5mXfEgOqb9o241MxS0SJKKFTuLf6yNsxdqq+9CyKf0btO9DJv6m7bH0aCWehU7OrtcH2pE2ZBuLxuA4I/kmZFq+dI62lynElCtTzOydK2PsHj4leWSbZEK09snzF034/rRv1DV6kUwxDiRTRMLtc2QiBdDcyCSv2tlVHRI7TFJFJ1Ok1wfYyeYVjrdswjgjceDbvPXvCYOuSDGefmSyefyNj6NRjueLn6hHOfTBNso4Pif5osG+KGfjjBrjkml+4FDZCjDYH5s8yTRuTYiVDcXKFI6H1Snmxbl/KhmXTEZXl7PN+pLp7LO9tz+SyTm+JJNzABTdk0yKYPaYIpl6ULvmGJLJOS4kk3MAFN0nMs1C+uIWv8Dxk7gwBw7lALetK16eDpoKgeK/eyAwk45k8gsmyeSHvbZnkkkb0YP2SKaDgF24O8nkHBySyTkAiu5JJkUwe0yRTD2oXXMMyeQcFx8y/Z1+//wx/fgR/vs1/ZdhYKHLHEzT1OtjtfP39/SzmPcOnZyGcntoMsXty/NJOP9sfW9cPMj0368f049fC4VQDueAbZTf0Uls0C7Kr3wsdv6bflUvAvPohk7OQr89MJm+pg94Y/zsN4S1QnE+mUIy/px+/13PILvKW+gkUr0+punv75/zavrz169iZWrp5Ays2gOTKYdkXqWAXLn2uq3TyZSRJ+ACyW2hk9D3+gg3h//9N83XgMJGWyenYNW+CZmW1+65bX1HmhSJOA6Z0tkV55A0YfkqVi3Qmopjkwn3NA22jylGlSvTTjJHwMJnizAtHdowkMcmEwDCunkARksskm1nMveOk3PRsFPYACctHXSzEG9DpmULM+vmvU4SIE/onCWfhU7OqNcH2MnmDMeL8xE64+a4ZApbluHWjivT/kzBx9EoBwvYRvkdnZwZ2kX5lY9kh2RKUCgJWKA9bBMYb1UKQJz+nWlGP6wOW3+0tdDJkPf6WO2QTBJQtgMCPmQi9hYIjHubZ4GGg02SyQF0I5ckkxGwe82STHuRun4/ksk5RiSTcwAU3ScyzQJrQMzfYYgF6z505wC3rSteng6aCkHjv3sgMBOQZPILJsnkh722Z5JJG9GD9kimg4BduDvJ5Bwcksk5AIruSSZFMHtMkUw9qF1zDMnkHBcfMvXWYOgdJ0Fu2Vn7Vl8Zao1r6aR/m/YtyDRvWQ8/Zf/5xwYlQ6seZMKXS1EOp4ltlN/RSfjQLsrf/eK7e3mxF+yL8qu5fdu1lcYnU9gg+PyYPp4k075UCYl61RoQrToPvfPeh4pGr8HJtLw5/vHFX1vfnQzF7RMkqYVOTqzlo1XnoTWupZP+DdtDk2newzTvaSKZdudIK/EsdHJiLR/YV/aT7b2FYNCmsTwumbLfMyWZdudJb1L2jpMTa9nBvrKfbJNMiNY7cry9izZIpojEy8/epOwdJyfUsoN9ZT/ZJpkQrXdk/EVt8VLmYLXzwq3Buf/gO1JwnCWphU6eXcsH9M3mFY63xrV0YNNYHPc2LwOGK1MGx4sGPlZGOQzDNsrv6OR00C7KWb+CTP1zy+waNkgmQ3D3mD5/ZQqzClfyq9aAWFGrkKl/3nsi8X6fm5DpfSC8LPiQyets7+2XZHKOL8nkHABF9ySTIpg9pkimHtSuOYZkco4LyeQcAEX3iUyzwBoQrAHBHHgvB7htXfHydNAUV6aDgF24e1qZLjzHW0+NZLpPeEkm51iSTM4BUHRPMimC2WOKZOpB7ZpjSCbnuJBMzgFQdE8yKYLZY8qHTK16CRY6iUzLx9q3+jpR7zjp36Y9MJmWl1vnE4iPc+HHz2zg0rfqQSZ8uRTlcHbYRvkdnUQN7aL83S++O7i/BsQytj7u266tNDyZBuRPFtHzydTarmChy073xVaK3hoQrXHSv12bZLLDdpfl08lU3D4BgSx0EoWWj94aEK1x0r9he3gyzScw3+bxZzh35UkrmS10clItH9hX9pNtuVkwji36RYX958BkysHhD0TneGy2imS71sqU5i3nKdskU4LKQFi2so/2HYq3eUBmzApJHtkmmRAtZXmuVjTerd7pZJJJmCWpSGwVnYxzywf0zXyH473jwKaxOOxt3tdHTpy5RPJgxVRCbM8nk83jb3zEjXItf1GPcta3IFN73mlsZVzSGQvDkmkKZZHj35fC54BECrH1IFN/LYWwOvTUjpBZ3LKz9q2Sonec9G/THpdMNnicbtWHTKef5j/hkGRyDjPJ5BwARfckkyKYPaZIph7UrjmGZHKOC8nkHABF94lMs4Bf6CnnDziIB/HYkwOsAaF4eTpoiivTQcAu3D2tTBee462nRjLdJ7wkk3MsSSbnACi6J5kUwewxRTL1oHbNMSSTc1x8yNTa/m2hkyC3fKx9q29AtHQ7bMppKLdJJmVAj5rzIBO+D4dymDu2UX5HJzFBuyh/94uvDeXb1hd9XYd2UP62aS8NT6ZlH1P89cD85Vd7+N73cD6ZQjL+nH7/XeeerQAWOolRy0d7+/nf3z+nHz9+TD9//Zp+/kCitW3KGVi1hybTTKRBX3CNAT2dTBl5wiwgES108UTjZ8vHi+3nf//7b5qvAdKGbOM5Rb8nfA5MprAZcLyVSMaUZAIyIzgFQUApdbJNMgFYe8R1M+DzGW/xHtNjtG22HlswWolnoZOxbPnAvkU/UEqdbJNMANYecd7PBCvTTK7HNBqfuDJxZdqT7rZ9ZjJ9TF/Jy5i/uH46meRVO7uqi8RW0aUArULLB/TNfMPxIBa6nTaFGe3muN+ZipoPJNPe5MBHxyiH8dhG+R2dnBfaRTnrVxAGtBUd2kEZRpmL45JpEuSRt33m0Ok4OH9lCvMOV/Ke7ee94yRWLTtr3wphkpWqbofNZMBGGJhM0zSt35Pmk3iM930phNSHTDbJ9K9bHZtMN4geyXSDIK6nQDI5x5Jkcg6AonuSSRHMHlMkUw9q1xxDMjnHhWRyDoCi+0SmWdizx519WAuBObCdA6wBoXh5OmiKK9NBwC7cPa1MF57jradGMt0nvCSTcyxJJucAKLonmRTB7DFFMvWgds0xJJNzXHzI1KqXYKGTILd8rH2rrwy9qZPTUG6TTMqAHjXnQSZ8ERTlMHdso/yOTmKCdlH+7hffs8Ot6VHbq4vj7T7HJZP8fab0uBa3ZdgBp2X5fDKFZLxbDYh27QitWL2yMy6ZKmc2/3rgYLsDTydTcfsE5LLQyTi1fPTWgHgxTk7Bqn0fMhX7m6wg07VLMgGZEdqCdKDs1YEJC/E2ZBpxVQoBJZlIJgtiv2EzVCrifqZdABZXdUhmC52cVMsH9i36gbJXByYsxFusTCPXzzt9ZbplDQigRoto0M1CvAGZxl2VQkDPJ5PN4298xI1yLWlRj3LWt0WKXl3mQL8xPJmW8shjPQ7HMHqQ6Z41IFZUW0RD4A3kwcm0rErPzz8G0Jxj0odM55zbv+ZlcDKNHy6SafwYxjMgmSISTp8kkxPwBm5JJgNQj5gkmY6gde2+JJNzfEgm5wAouk9kmoX0sij8sgSPbe/3JzbERuYAa0AoXp4OmuLKdBCwC3dPK9OF53jrqZFM9wkvyeQcS5LJOQCK7kkmRTB7TJFMPahdcwzJ5BwXksk5AIruSSZFMHtM+ZCpVdDEQreBTPU9uhP9b0yr9/DYZBJ1IEZ8R8+DTPimNsohibCN8ju6enKGfVThB9fyoinoE2V9//VZvXN0YDKFl1zlD0RD+x1UThx7PplgM2A4z2x1sNCVYP79/XP68ePH9PPXr+lnRqZz/Jcz0jkyLpnmmg+49UKQSwcfcyunkykjTzg9SGALXQXBv//9N/0Nx6U/2daYW8W/1aFxyTRN01z34REIJX7f1gotA7v/IpkSjJI8sk0yJahOERZCPabH83MacVcTyQTfmUimUzhTcZJvV1923PI7UwWo/JBFwrZs5t7zlhwn21yZcrysWmURlTFv9U5fmTBBQ3CyBIbvT2q6RgZkvkO/k/03ptajGvc70/xYHB5AzA8kxiv3dT6ZbB5/42NslJtJWZDJZm7NOSgqxyVTegDxvV2Ef2famxlhBQh/4yn/zmNTbGVjXhUynep/Y1q9h4cmU+9JX2mcx8p0pfO/01xIJudokkzOAVB0TzIpgtljimTqQe2aY0gm57iQTM4BUHSfyDQLcj8726xxwBw4lgOsAaF4eTpoiivTQcAu3D2tTBee462nRjLdJ7wkk3MsSSbnACi6J5kUwewxRTL1oHbNMSSTc1xIJucAKLonmRTB7DHlQyaLOgstmxvIVF8natlp6VYfVZsb/pUPj02mrAbEeNsvQiw9yIQvoqIc5oNtlN/R1XM2vh8I+5ne8L/4qNus+9c/Oi6ZZiIBgeRb5PpYmVg8n0wW2xxaNkvY9GtAhJ0kW3UlSv9WR4YlU7mfiTUgdiVJcRsERLDQVSalXgMibMvaqitR8W91aFgyTcVKlO+8tQJM2+7pK5MFYVo2W4DJcbKNmwVbOvRR9EOlrTwumYr9TM/p+eTmwJfpUiTb+StTmqOci2yTTAmqkwWuTLsA703Y3nGtSUmbsk0ytdAz1BW3fYa+FE2ffpuHCRrOI0tgWKXUdA2wMt+hX69/8FHYBJ2xOPRt3jc2y6rEbevfiLQkfOSNchiDbZTf0W3OpZL46BPlV/6Tj4rNpDMWxiXTWkBlPoHHYxqRSCG2569MwWtYAe5WA2JlCslkfMm4sHkfMl0YkIGnNu7KNDDoOHWSCdEYWyaZnONHMjkHQNE9yaQIZo8pkqkHtWuOSWSaBe73P7bfn3gRL5kDrAHhd6XjyuSHvbbntDJpG6a9fQiQTPtwGqEXyeQcJZLJOQCK7kkmRTB7TJFMPahdcwzJ5BwXksk5AIruSSZFMHtM+ZCpVUvBQreBTPXVn5b/1U7vuI1paB0ejkzLz21W3sUT7+p9fGlBZGvHg0z4AinK4UyxjfI7ujqC8f3A/TUgFju94+qz0Dw6EJnim+Ff0+dTkinq1p+IlvUhNBFTtnU+mXq3OfSOKwHbrtfQ8tGq89AeV87A5shAZIoAVH67ttjLtPQZYXU6nUzFLRIkooUuhg0+N+s1tPy36jy8GAeuTcVbkKksrlIhnCmM/cb/RTIltCQJZFtuFowDZT/Z3hoXxxt93pRM0/T1IW8FjRB80yzJBN+Z9pJC9pNtkmlvVparDlemvdjJbeph3Pm3eWm2kgSyjXNLgyrnsHcc2jCQb7EylWW/+J1pO1eAPKFTlogWuu2Z5L5Dv5Z/sJPN+cA4MGEh3oNMk6hMVDyQsIBOx+bpt3lGj7/xMTrKTZQKUrQfzSdbveOSARthIDIthJknDK+9p9oP2d+ZoGyyDW5qVj3ING4NiBX2Cpna56QWrqahgcjUPI9hlT5kGhauS0+cZHIOD8nkHABF9ySTIpg9pkimHtSuOYZkco4LyeQcAEX3iUyzAF/s2X6wvgHz4XgOsAaE4uXpoCmuTAcBu3D3tDJdeI63nhrJdJ/wkkzOsSSZnAOg6J5kUgSzxxTJ1IPaNceQTM5xIZmcA6DonmRSBLPHlA+ZWnUWLHQbyFRfC2r5X+1Ux+3QbUxD6/BwZNqsATFNU0unBZi2HQ8y4YuoKIdzwzbK7+jqmIU3xMNvRMF+phf+Fzv1ca919VloHh2ITLHOQ6sGRE2nCZe+rfPJ1NrmYKErMdOvAdGqD1H6tzoyEJkiBOXmwKiZppbuu9eVpNPJVNwiAYEsdBWw1WtAtOpDVPxbHSKZrJDdafdfJFOCRpJXtuVmwTiw6BcVcrMjHD9BJJlOALnlgmSC70wFSWDVRBCLfqBs6aCbhUgyWaB6wCbJRDIdSBftrq3vRS2d9jx07J1OJnnrlF3JxUqgomvglNkP/Vr+wU4xbqcOulmIXJksUD1g83wy2Tz+xsfoKDehqJACx6Kc2amMS/qWLnWyEQYiU6sGREtnA5yWVQ8yteslhNUh/P2n/BtQ/7gNtKqJ3/K/2qmO26HbmIbW4YHIpHXK17LjQ6ZrYXCX2ZBMzpEkmZwDoOieZFIEs8cUydSD2jXHkEzOcSGZnAOg6D6RaRa45//4nn9iRswwB1gDQvHydNAUV6aDgF24e1qZLjzHW0+NZLpPeEkm51iSTM4BUHRPMimC2WOKZOpB7ZpjSCbnuJBMzgFQdE8yKYLZY8qHTK06Cxa6DWQOvxbUO7cN/8qHhyPTVp2HeHw+ocdjGuGX1kMsPciEL5CiHOaDbZTf0dVzNr6DB1swUse6DueD8qu5JbPGwkBkatSACD909vyc/qxgLcT6mL6MwdMwfz6ZQqL+nH7/XWefrQ4WuhKl7RoQrVoOvXMr/VsdGYhMEYIde5bmXxEc49cDTydTRp6AKSSphS6GDT43a0C0ajn0zg38Wov3JBN/03Y7b3qTsnfc9kzEj1OLjtKfbO+9CAizls0bkmnHymWJ6EHb/+LKlCAqCJI0JdGKvjtXVDBpLd6OTF8fj+kB35+sAXzXPslUewBRqTJEMr2barXx2yvPaEQKZ3c6mfD2KEwgS1K42qvpajFcj2W+Rb9C1zs3YdeweZOVaSHYSCtSjOn5ZLJ5/I2PqlGO51n9LAgDvSo6tItyGIVtlMGiuTgQmRp1HuYHDpWfzRzgj00eZOqv5RBWh576EBt5XCFM6lnVKftPznSEgcikc8JXs+JDpquhcI/5kEzOcSSZnAOg6J5kUgSzxxTJ1IPaNceQTM5xIZmcA6DoPpFpFnAvO2XWNmAOHM8B1oBQvDwdNMWV6SBgF+6eVqYLz/HWUyOZ7hNeksk5liSTcwAU3ZNMimD2mCKZelC75hiSyTkuJJNzABTdk0yKYPaY8iFTby2F3nEbyFRfGVr7VnUt/61xG/6VDw9Hpljr4fkZN6kviMTj8wk9xtiyHmbuQSZ8ERTlMB9so/yObomQ/H98z662BaOuw/mg/G25Pu5bbysNRKZGDYjpa/qAPUzzVowBXnINoT2fTCHh7lYDolU7wpZAaH0gMsVpb+9nSj0+n8NsEDydTMXtE5DLQheDAp/qNSBatSPAr7V4QzLFFSy/DbQGstf+v0imhFVB3qQRmxblJsbQDy4CMCzf7IgKe/k+ZMI9TYPc4oXwkky170wV8hTEI5kULg87b/MGeQhBMpFMCqToNfGaTBPr5jXAFVf07IpvoWtMJfMt+hW61txgbDEOdMbiPW7zAnng1o4VXdtZg4+VUQ6jsI3yO7rN2bQSv6LD+aCc2a+My/SGjYHI1KgBMa0FVdKWgTGquYa4nn6bNydTuMr31HLoHbeRwa3Er+pa/lcf1XEb/pUPD0Qm5TO/iDkfMl3k5G82DZLJOaAkk3MAFN2TTIpg9pgimXpQu+YYksk5LiSTcwAU3ScyzUL6Al8p6Ejd/LCAODE3mjnAGhCKl6eDpkJg+O8eCMwkI5n8gkky+WGv7Zlk0kb0oD2S6SBgF+5OMjkHh2RyDoCie5JJEcweUyRTD2rXHEMyOcfFh0ytWgoWug2QW6/+HNa15r3hX/nwcGSKtR5kDYiIy7xl/fGYtvSx31U+PciEL4miHDDBNsrv6OpYx/fsalswjutwrijXfdscHYhMcQft1/T53CBL2CD4/Jg+tvQ2GL5l9XwyhUQdsQZEq85D65zeCs+hwQORKZ7X1n6m5fjH15Y+jr/W5+lkKm6fIBEtdBW4u2pAtOo8tOZd8W916DZkmm//5j1NJFMzWVqJZ6FrTabwB52P6Iq+cIEAk9biPcg076yNtfJIpmbStBLPQteaTOEPOh/RFX1JJkCyJUqyLO3vjbZS37Llr/sXb/MS6gUJkqasTgSqogJRYYdkQrgasiRLfQfuvORCYcqGQVfV6WSSJbKyRBRJqKJrwJvZF/0O6VrzFnYNm/e4zcsAkmTLlJdrnE8mm8ff+Dga5SbghwgDlirj0CfKMMpcHIhM9RWo/HsSyfQ6a8KVfMQaEOuZVci0FKXcOqfXiGj0GIhMGqd7PRseK9P1ULjHjEgm5ziSTM4BUHRPMimC2WOKZOpB7ZpjSCbnuJBMzgFQdJ/INAus88A6D8yB93KA29YVL08HTXFlOgjYhbunlenCc7z11Eim+4SXZHKOJcnkHABF9ySTIpg9pkimHtSuOYZkco4LyeQcAEX3JJMimD2mfMjUqpdgodtApvpa0NrXQrcxDa3Dw5GpXgNieR9vPpn4aPd7T4YWViZ2PMiEL4KiHE4Q2yi/o6sDF98P1KkBsfho2azPQvPoQGRq1YBYyDQIf7L4nU+m1nYFC112unPj7++f048fP6afv35NP3/kZLLQlTOwOTIQmSIAtbfCSaaIzsvP4vYJCGShq0xIvQZEqz5Exb/VoVuRaT6Z+TaPP8O5mTAWhGnZ3JxIYMDvYmVK3S10ybiNcBMy5eDwB6JzPLJWkaTnr0xpPsVcksaGaGDeQgjzv4wAAArvSURBVLwlmaZp+X41wneoEIBT/xUJTDJp4X9PMs3Visa41TudTLesAQF0KC4WoDMWb0Gmr4+cOHOJ5AGKqYTYnk8mm8ff+Bgd5Wb+thLfQteczPvKgcjUqAERyiLHvy+Fz0GI5EWmdr2EcNu3VUuhV7eRqBaEadncmIbW4YHIpHXK17LjsTJdC4H7zIZkco4lyeQcAEX3JJMimD2mSKYe1K45hmRyjgvJ5BwARfeJTLOAX+Ip5w81iAfx2JMDrAGheHk6aIor00HALtw9rUwXnuOtp0Yy3Se8JJNzLEkm5wAouieZFMHsMUUy9aB2zTEkk3NcSCbnACi6J5kUwewx5UMmwzoPu17nsfDfstkTmeNjhiNTvQbEcuJRN5/UI3/59Tg054zwIBO+iIpyOGNso/xKt6AV393Lt6JLJNEuyq98YF+UX42T/q3aA5GpVQNimmYiDfSCawzo+WSC/UthEtlK0qsLZrbrOsRzXT57ffSOy71btgYiU4ShVgMiEG2MlSieRfw8nUwZecIsIEl7dUdqMPT66B0XgT7h8x5kWjcDPp+P77/Sj7DN1mM/U29StsZhohb9UClXwqBTIHPhE2wK95bNe5Bp3s8EK9NMrsc0Ap/usjKlJC0SO2kWodBD4lvohHvL5o3I9DF9JaRqt4JJeSmBZCKZHBOyQpSi5kOlj+OMW65PJxPeVoWJZasBJPYhHZxhZg+OJ7HXR++45NhcuMfKNAnyyNs+cxj7HZxPpv7H3/g4GuXs7F+SycY/zgflbG7GjYHI1KgBEUBavyfNJ/QY4/tSmLYHmWxqQKyZuoNMNv7DyrVVu8KYRav5gch0DiBne/Eh09ln+W/4I5mc40wyOQdA0T3JpAhmjymSqQe1a44hmZzjQjI5B0DRfSLTLOzZ484+329ZEAtiIXOANSAUL08HTXFlOgjYhbunlenCc7z11Eim+4SXZHKOJcnkHABF9ySTIpg9pkimHtSuOYZkco4LyeQcAEX3JJMimD2mfMi0vMs4B/+Bb9uHM7DQbSAzvwKm5X/1UbW54V/58HBkinUenp9/vqGQv8+UHlfKQH0PuYrkQab5x+DWzV4oB0ywjfI7ujrW8V3LPEboE+VX/hcfdZt1//pHByLTAtTz82v6fD6mjEwVXGQgKl0uceh8MgUc5UbKmNAWuhLmdEH8+Jie2crY63+tAfJ4TM/CZunf6shAZIoQiO0W8TB+FvubUHkt+XQyFbdBkMAWugrcf76+pvm+QvqT7fmHvlfit3Th5nTLZsW/1aFbkmmUVSkE9V8kU0pmSRDZPkCmTZtJYS/ckEzhSsv9TJup05uwveM2JxL3oMVbzEqbZGqhp6Fr3+aNVj+PKxPJpMGKThstMo21KgUATicTXu3DBLIVB74/qekaYc58h369/sFHYRN0xuKtbvOWp0RwpTMGT8P8+WSyefyN31NRbmJUSXwci3Kwg22UMx8Vm5nesDEQmZZVZ55w+jsSPiJf9K8emRti2WXag0zLChALdsqLD+KspduAppr4vf5XH1WbG/6VDw9EJuUzv4g5HzJd5ORvNg2SyTmgJJNzABTdk0yKYPaYIpl6ULvmGJLJOS4kk3MAFN0nMs0CfLFnO35B5ydz4UAOsAaE4uXpoKmQqPx3DwTmiw7J5BdMkskPe23PJJM2ogftkUwHAbtwd5LJOTgkk3MAFN2TTIpg9pgimXpQu+YYksk5Lj5kMqzzsOt1nl7/a7CqPlo2zwnycGRKW56xBkTAStSBGOUdPQ8y4UuiKC8wPqZHR32IJV3je3Xynb48mdEnyq/8t3ygHZRzz7atgcgUX2St1YAIOlnXANq2GL5l/Xwy1bCKyd+rO1KDwcJHy+Zb4Tk0eCAyxfOq7Gcqln0Bbhx6wc/TydTCqld3pAaDhY+WzRNjfg8yxb0uc6WbCtlOBPSoq7uQKZ13kdhJswiFHi58LR2akf1kW24yxLGG8m3IFDCa75XDK1HPz6X6jSFwWqZJJpJJK5c67NRWnhCQ7yIqy0MKfmeqgtu6ivfq0FFhA5Vym3zQkUwCoTObJZnKIiplnzNneMTX6SsTJm+YaJb8kNiHdHDGmT04nkQLHy2bybG5cI/bvPmxeHwiFRPke6UyR/ENB+eTqV1LAR8roxxOEdsoZ6f/kkxtO2gX5Vc+sC/K2TjjxkBkClef8lX4+PekGUDQx+PG+L1t3oNMNjUgVih2kKnff8sH5gdcWN+O0H4DA5Fp/0mN1NOHTCMhNM5cSSbnWJFMzgFQdE8yKYLZY4pk6kHtmmNIJue4kEzOAVB0n8g0C/AFnu3yYQcxISYvc4Db1hUvTwdNheDw3z0QmIlGMvkFk2Tyw17bM8mkjehBeyTTQcAu3J1kcg4OyeQcAEX3JJMimD2mSKYe1K45hmRyjosPmZYXgefgZ792HsDo1a1A7nqdyNDHLv82QR+OTPtqQIyx/SKE1INM+CIoymE+2Eb5lW5Jz/h+XPvdOLSL8vs+9vlf5qr//4HItAD1/KzUgJjfGgcCybfI9XFTs3g+mQKOgFV2Je/VedeAOOJfLXSFoYHIFOde7lUq9zOJpIhDL/h5Opky8gRAAKteXbg5/PpadjcXNgTohX6n/xc+dvsX09Fs3oJMS5kvvLUIAeJ+pmqi9CZzaxw6KvqhMu41k7FaV8piLBANzRT9QNnSQTcL8R5kivf66XWo5/R8kkzVhCmSDRK2V4eOChuoJJkEGt7N8javnBFXphKT9UiR7CTTJlYHFbdZmbLz5gOIDI68AeQJioxcvTrwkNmD40k09vHSf5qIunBDMoVgPSZuW9/OFXwcjXIYgW2UX+mStx3JjHZRVvGxw3+aq7IwEJkWkswTTt+NVtLMAH5vDxiFSCGW4XzO/4dY4sOAMJNe3XoWu5LZ0Mcu/zaID0QmGwC8rfqQyfus7+mfZHKOK8nkHABF9ySTIpg9pkimHtSuOYZkco4LyeQcAEX3iUyzAF/s2f5+oEEsiMXuHOC2dcXL00FTIUj8dw8EZsKRTH7BJJn8sNf2TDJpI3rQHsl0ELALdyeZnINDMjkHQNE9yaQIZo8pkqkHtWuOIZmc4+JDpt4aDK1xK5C7XufptdMa19KdE+ShyBTrP8yTlpv/xPt5H1/nAPiuFw8y4culKIdzwTbKr3QLDvGdO/m+X44S2kX5u1fdDvZFed/cvq1bSeOQKZAFfvh5IVYM2gJ+esFV1oSwQk/B7vlkClhdtQZEq5ZD77wVgrTTxDhkkic0r0RrUhT7l5Ylf4TV6XQyFbdhkKS9uhf1GbLQtXy07LTGtXSZc9vGuGQCApUFVRYypZXKFsO3rN+FTAmEIrGTZhEKPZAZu8p+sr23EAzaNJYHJVNOlpJMy70/yVTJnt6kbI1DN0U/VMqdvUFHMgmEzm3OXz7l9ydox6qkJFMlLkWyQzL36tBNYQOVJJNAw7cpiTTPBm75ltnxO9N2lIA8oVOW/L068JbZg+NJbPlIncS8wvHWuJYObBqLA93mLQR5ZCtQRCeACaW9CnLFftf7PP070xuPv/FxNMoZqi/J1H78nmxV7KBPlMMYbKOc7J0gjEOmmSCVrQDxkd0MftTDo98TQHzHhQeZ+us8LBetOWmKgv8rChUSlPj02mmNa+nKGVgcGYdMFmd/AZs+ZLrAid9wCiSTc1BJJucAKLonmRTB7DFFMvWgds0xJJNzXEgm5wAouk9kmgXWgJiLQhKL+CCHn0dz4f8BxAwLnPM8M58AAAAASUVORK5CYII=[/img]
Ada yang bertanya tanya gimana caranya ? Nih ane punya cara gampang banget Gan/Sist.

Konversi Bilangan Desimal ke Bilangan Biner
Misal ane ambil contoh bilangan desimal 17 itu bilangan binernya 10001 atau kalau mau di panjangin jadi 8 Byte 000010001. Cara penulisan binernya diurutkan dari hasil bagi paling bawah yaitu angka 1 dari hasil bagi 2/2 terus ke sisa paling bawah dan berurutan ke sisa paling atas.
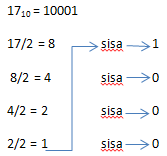
Konversi Bilangan Biner ke Desimal
Misal ane ambil contoh bilangan 12
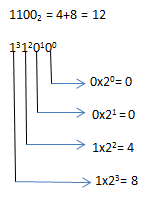
Nih kita kasih pangkat nol dari angka paling belakang ke depan berurutan. Dari gambar diatas udah jelas kan Gan/Sist yang ada hasilnya di jumlahkan aja
4+8 =12.
Sekian pembahasan bilangan biner dari ane, Agan Sista bisa bisa coba-coba sendiri buat latihan
 Untuk pembahasan selanjutnya di tunggu thread berikutnya.
Untuk pembahasan selanjutnya di tunggu thread berikutnya. Semoga bermanfaat ya


0