TS
Bridge Engineer
Tempat Nongkrongnya Pemerhati Mekanika Teknik/Analisis Struktur
- Struktur Pembahasan Thread
- Pengantar Mekanika Teknik
- Dasar-dasar Struktur Statis Tertentu
- Beberapa Contoh Struktur Statis Tertentu
- Balok Sendi-Rol Dengan Beban Terpusat
- Reaksi Perletakan Balok Sederhana
- Analisis Balok Sederhana
- Analisis Balok Sederhana (lanjutan)
- Struktur Balok Miring Sederhana
- Semi Portal Dengan Beban Merata dan Terpusat
- Portal Dengan Beban Terpusat dan Merata
- Struktur Balok Gerber
- Struktur Balok Gerber Pada Konstruksi Parabola
- Struktur Balok Gerber Pada Konstruksi Lingkaran
- Struktur Balok Gerber Pada Konstruksi Lingkaran (lanjutan)
- Struktur Balok Gerber Pada Konstruksi Lingkaran (lanjutan)
- Struktur Balok Gerber Pada Konstruksi Lingkaran (lanjutan)
- Pertanyaan Bagus
- Jawaban (1)
- Jawaban (2)
- Jawaban (3)
- Tanya Lendutan
- Pertanyaan bagus dan jawabannya
- Pertanyaan bagus dan jawabannya
- Pertanyaan bagus dan jawabannya
- Pertanyaan bagus dan jawabannya
- Pertanyaan bagus dan jawabannya
- Pertanyaan bagus dan jawabannya
- Pertanyaan bagus dan jawabannya
- Pertanyaan bagus dan jawabannya
- Pertanyaan bagus dan jawabannya
- Pertanyaan bagus dan jawabannya
- Pertanyaan bagus dan jawabannya
- Pertanyaan bagus dan jawabannya
- Pertanyaan bagus dan jawabannya
- Pertanyaan bagus dan jawabannya
- Tips Membaca dan Memeriksa Diagram Gaya-gaya Dalam
- Struktur Rangka Batang
- Contoh Bangunan Struktur Rangka Batang
- Tipe Struktur Rangka Jembatan
- Kriteria Desain Jembatan dan Contoh Tipe Rangka Jembatan
- Lanjutan Kriteria Desain
- Kriteria Keruntuhan Struktur
- Asumsi Dasar Analisis Struktur Rangka
- Lanjutan Asumsi Dasar dan Teori Dasar Banget
- Struktur Rangka Batang dengan Kabel
- Struktur Rangka Batang dengan Kabel (lanjutan)
- Struktur Jembatan Rangka Dengan Beban Terpusat
- Struktur Jembatan Rangka Dengan Beban Terpusat (lanjutan)
- Struktur Jembatan Rangka Dengan Beban Terpusat (lanjutan)
- Struktur Jembatan Rangka Dengan Beban Terpusat (lanjutan)
- Struktur Jembatan Rangka Dengan Beban Terpusat (lanjutan)
- Struktur Jembatan Rangka Dengan Beban Terpusat (lanjutan)
- Struktur Jembatan Rangka Dengan Beban Terpusat (lanjutan)
- Struktur Jembatan Rangka Dengan Beban Terpusat (lanjutan)
- Struktur Jembatan Rangka Dengan Beban Terpusat (lanjutan)
- Struktur Jembatan Rangka Dengan Beban Terpusat (lanjutan)
- Stuktur Jembatan Rangka Dengan Beban Simetris
- Struktur Rangka Atap Bangunan
- Struktur Tower dan Crane
- Hal-hal Penting Tentang Analisis Struktur Rangka
- Catatan Dengan Metoda Ritter atau Potongan
- Garis Pengaruh Struktur Sederhana
- Dasar Teori Metoda Elastisitas
- Lendutan Balok Sederhana Akibat Beban Terpusat Dengan Metoda Elastisitas
- Lendutan Balok Sederhana Akibat Beban Merata Dengan Metoda Elastisitas
- Lendutan Balok Sederhana Dengan Beban Asimetrik
- Lendutan Balok Sederhana Dengan Beban Asimetrik (lanjutan)
- Struktur Balok Sederhana Dengan Beban Segitiga
- Balok Dengan Dua Beban Terpusat Menggunakan Metoda Elastisitas
- Balok Gerber Dengan Metoda Elastisitas
- Hubungan Teorema Maxwell-Betti Dengan Metoda Elastisitas
- Analisis Balok Menerus Dengan Metoda Conjugate Beam
- Analisis Struktur Rangka Dengan Metoda Matriks
- Analisis Struktur Rangka Dengan Metoda Matriks (verifikasi)
- Balok Sendi-Rol Dengan Beban Terpusat
- Analisa Penampang Profil
- Struktur Statis Tak Tentu
- Dasar Teori Struktur Statis Tak Tentu
- Dasar Teori Struktur Statis Tak Tentu (lanjutan)
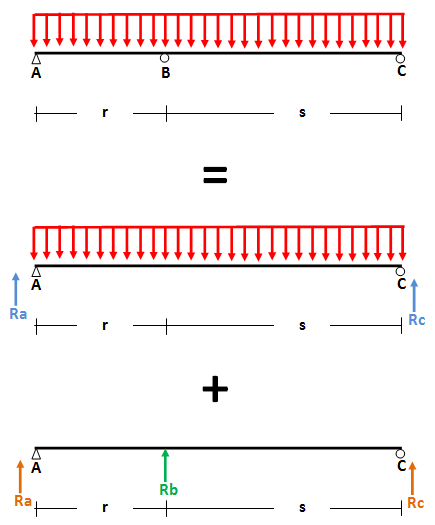
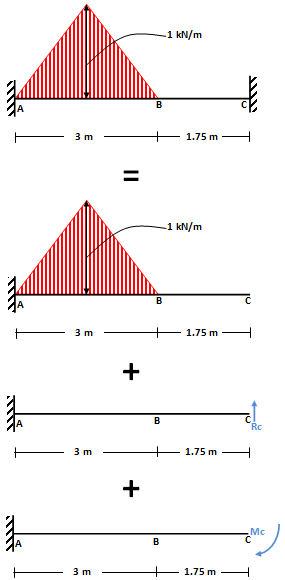
- Prinsip Superposisi Analisis Struktur
- Prinsip Superposisi Analisis Struktur (lanjutan)
- Prinsip Superposisi Analisis Struktur (lanjutan)
- Struktur Portal
- Struktur Portal (lanjutan)
- Dasar Teori Metoda Slope Deflection
- Dasar Teori Metoda Slope Deflection (lanjutan)
- Struktur Portal Dengan Metoda Slope Deflection
- Struktur Portal Dengan Metoda Slope Deflection (lanjutan)
- Struktur Portal Dengan Metoda Slope Deflection (lanjutan)
- Struktur Portal Dua Sendi Dengan Metoda Slope Deflection
- Portal Beban Terdistribusi dan Terpusat Dengan Metoda Slope Deflection
- Struktur Portal Dua Sendi Dengan Metoda Distribusi Momen
- Koefisien Momen Balok Menerus Berdasarkan Metoda Distribusi Momen
- Portal Beban Merata dan Terpusat Dengan Metoda Distribusi Momen
- Keterangan Tambahan Mengenai Metoda Distribusi Momen
- Keterangan Tambahan Mengenai Metoda Distribusi Momen (lanjutan)
- Analisis Balok Menerus Terjepit dengan Metoda Slope Deflection
- Dasar Teori Metoda Energi
- Dasar Teori Metoda Energi (lanjutan)
- Dasar Teori Metoda Energi (lanjutan)
- Dasar Teori Metoda Energi (lanjutan)
- Dasar Teori Metoda Energi (lanjutan)
- Dasar Teori Metoda Energi (lanjutan)
- Struktur Rangka Dengan Metoda Energi
- Struktur Rangka Dengan Metoda Energi (lanjutan)
- Struktur Rangka Dengan Metoda Energi (lanjutan)
- Struktur Rangka Dengan Metoda Energi (lanjutan)
- Struktur Rangka Dengan Metoda Energi (lanjutan)
- Struktur Rangka Dengan Metoda Energi (lanjutan)
- Struktur Rangka Dengan Metoda Energi (lanjutan)
- Struktur Rangka Dengan Metoda Energi (lanjutan)
- Struktur Rangka Dengan Metoda Energi (lanjutan)
- Metoda Elastisitas Pada Struktur Terjepit Di Kedua Ujungnya
- Struktur Balok Menerus Dengan Metoda Elastisitas
- Struktur Balok Menerus Dengan Metoda Elastisitas (lanjutan)
- Struktur Balok Menerus Dengan Metoda Elastisitas (lanjutan)
- Struktur Balok Menerus Dengan Metoda Elastisitas (lanjutan)
- Dasar Teori Metoda Persamaan Tiga Momen
- Dasar Teori Metoda Persamaan Tiga Momen (lanjutan)
- Struktur Portal Dua Sendi Dengan Metoda Persamaan Tiga Momen
- Struktur Portal Dua Sendi Dengan Metoda Persamaan Tiga Momen (lanjutan)
- Struktur Balok Terjepit Pada Kedua Ujung Dengan Metoda Persamaan Tiga Momen
- Struktur Balok Terjepit Pada Kedua Ujung Dengan Metoda Persamaan Tiga Momen (lanjutan)
- Struktur Balok Terjepit Pada Kedua Ujung Dengan Metoda Momen Area
- Struktur Balok Terjepit Pada Kedua Ujung Dengan Metoda Momen Area (lanjutan)
- Dasar Teori Struktur Statis Tak Tentu
- Sepintas Tentang Dinamika Struktur Jembatan
- Frekuensi Alami Struktur
- Frekuensi Alami Struktur (lanjutan)
- Frekuensi Alami Struktur (lanjutan)
- Frekuensi Alami Struktur (lanjutan)
- Frekuensi Alami Struktur (lanjutan)
- Ilustrasi Permasalahan (1)
- Ilustrasi Permasalahan (2)
- Ilustrasi Permasalahan (3)
- Frekuensi Alami Struktur
- Beberapa Contoh Kasus
- Penanganan Kerusakan Jembatan Katingan (Prov. Kalteng)
- Penanganan Kerusakan Jembatan Katingan (lanjutan)
- Penanganan Kerusakan Jembatan Katingan (lanjutan)
- Penanganan Kerusakan Jembatan Katingan (lanjutan)
- Penanganan Kerusakan Jembatan Katingan (Prov. Kalteng)
- Obrolan Santai
- Pertama
- Kedua
- Ketiga
- Keempat
- Kelima
- Keenam
- Ketujuh
- Kedelapan
- Kesembilan
- Kesepuluh
- Kesebelas
- Dokumen Pemeriksaan Jembatan
- Pertama
- Kepustakaan
- Sumbangan Kaskuser
- Dokumentasi Fabrikasi Struktur Jembatan yang TS Kunjungi di Luar Negeri
ngindeksnya masih dilanjutin...
selalu update untuk setiap pertanyaan/komentar tentang analisis struktur.
Diubah oleh Bridge Engineer 22-10-2017 17:45
febrinx dan 8 lainnya memberi reputasi
9
417.1K
1.9K
Komentar yang asik ya
Mari bergabung, dapatkan informasi dan teman baru!
Sipil
1.8KThread•884Anggota
Tampilkan semua post
TS
Bridge Engineer
#451
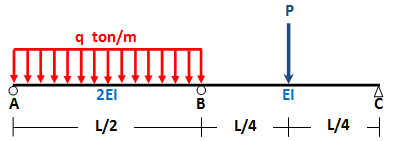
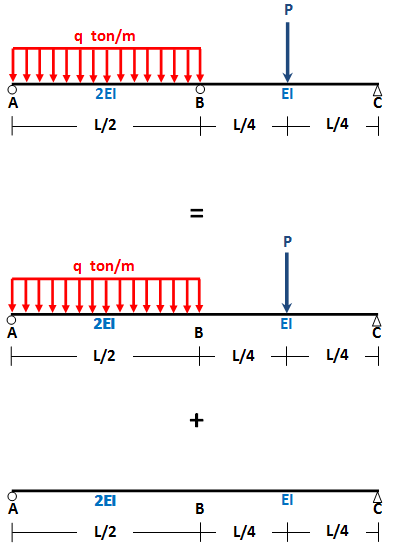
bahasan sebelumnya,
kita lanjutkan lagi...
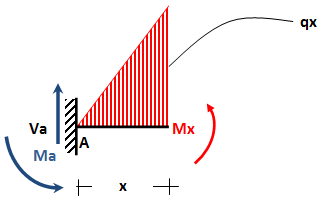
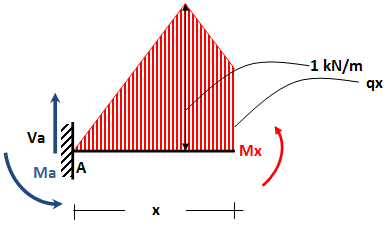
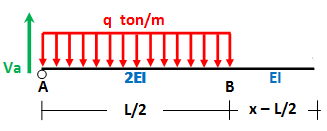
penerapan persamaan euler-bernoulli pada segmen L/2 ≤ x ≤ 3L/4
-2EI y'' = Mx
-2EI y'' = L^2 q/8 - L q x/8 + P x/4
-EI y' = 1/16 * L^2 q x - 1/32 * L q x^2 + P x^2/16 + U
-EI y = 1/32 * L^2 q x^2 - 1/96 * L q x^3 + P x^3/48 + Ux + V
Selanjutnya untuk potongan sebelah kanan, lihat gambar di bawah ini,
untuk 0 ≤ x ≤ L/4
Mx = (Vc)(x)
Mx = 1/8 * (q L + 6P)(x)
M(0) = 1/8 * (q L + 6P)(0) = 0
M(L/4) = 1/8 * (q L + 6P)(L/4)
M(L/4) = L^2 q/32 + 3 L P/16
M(L/4) harus sama dengan M(L/4) dari segmen lainnya,
penerapan persamaan euler-bernoulli,
EI y'' = Mx
EI y'' = 1/8 * (q L + 6P)(x)
EI y' = 1/16 * L q x^2 + 3 P x^2/8 + C
EI y = 1/48 * L q x^3 + P x^3/8 + Cx + D
untuk potongan selanjutnya, perhatikan gambar di bawah ini,
untuk L/4 ≤ x ≤ L/2
Mx = (Vc)(x) - (P)(x - L/4)
Mx = 1/8 * (q L + 6P)(x) - (P)(x - L/4)
Mx = L P/4 + L q x/8 - P x/4
M(L/4) = L P/4 + L q (L/4)/8 - P (L/4)/4
M(L/4) = L^2 q/32 + 3 L P/16
M(L/2) = L P/4 + L q (L/2)/8 - P (L/2)/4
M(L/2) = L^2 q/16 + L P/8
ok cocok dengan M(L/4) dan M(L/2) dari segmen sebelumnya,
penerapan persamaan euler-bernoulli,
-EI y'' = Mx
-EI y'' = L P/4 + L q x/8 - P x/4
-EI y' = L P x/4 + 1/16 * L q x^2 - P x^2/8 + R
-EI y = 1/8 * L P x^2 + 1/48 * L q x^3 - P x^3/24 + Rx + S
syarat batas yang dimiliki adalah
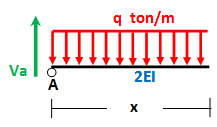
segmen AB 0 ≤ x ≤ L/2 dengan sebagian segmen CB L/4 ≤ x ≤ L/2
y(0) = 0
-EI y = 1/96 * x^3 (3 L q + 2 (P - 2 q x)) + Ax + B
0 = 1/96 * 0^3 (3 L q + 2 (P - 2 q * 0)) + A * 0 + B
B = 0
y'(L/2) segmen AB = y'(L/2) sebagian segmen BC
1/96 * x^2 (9 L q + 6 P - 8 q x) + A = 1/16 * L^2 q x - 1/32 * L q x^2 + P x^2/16 + U
1/96 * (L/2)^2 (9 L q + 6 P - 8 q * (L/2)) + A = 1/16 * L^2 q * (L/2) - 1/32 * L q (L/2)^2 + P (L/2)^2/16 + U. . . . . . . . . . . . . . . (persamaan 1)
y(L/2) segmen AB = y(L/2) sebagian segmen BC
1/96 * x^3 (3 L q + 2 (P - 2 q x)) + Ax = 1/32 * L^2 q x^2 - 1/96 * L q x^3 + P x^3/48 + Ux + V
1/96 * (L/2)^3 (3 L q + 2 (P - 2 q * (L/2))) + A * (L/2) = 1/32 * L^2 q * (L/2)^2 - 1/96 * L q * (L/2)^3 + P (L/2)^3/48 + U * (L/2) + V. . . . . . . . . . . . . . . (persamaan 2)
baru terbentuk 2 persamaan...
nanti dilanjut lagi....
hasil di atas belum tentu benar...
nanti di cek lagi...
silakan agan/sist mau ikutan periksa lagi atau sekaligus menyelesaikannya...
ditunggu...
Spoiler for sebelumnya:
setelah memahami contoh soal dalam pembahasan sebelumnya,
setelah membaca posting sebelumnya :
dan permintaan dari sista avalokitha,
kita coba menjawab nomor 1 di atas, perhatikan gambar di bawah ini :
struktur di atas termasuk statis tak tentu derajat 2, oleh karena itu ada 2 redundant. TS pilih gaya reaksi di C Rc dan momen gaya di C Mc sebagai gaya kelebihan.
Analisis untuk struktur statis tertentu pertama
supaya gak bingung saat menganalisis struktur statis tertentu yang pertama, TS berikan ilustrasinya supaya lebih jelas. Untuk potongan pertama perhatikan gambar di bawah ini :
0 ≤ x ≤ 3/2
qx = x/(3/2) * 1
qx = 2x/3
Mx = (Va)(x) - Ma - 1/2 * x * qx * x/3
Mx = (3/2)(x) - 9/4 - 1/2 * x * 2x/3 * x/3
Mx = -x^3/9 + 3x/2 - 9/4
periksa :
M(0) = - 9/4 = Ma
M(3/2) = -(3/2)^3/9 + 3(3/2)/2 - 9/4
M(3/2) = -3/8 kNm
hasil Mx ini harus sama dengan Mx dari potongan kedua di bawah,
penerapan persamaan euler-bernoulli,
-EI y'' = -x^3/9 + 3x/2 - 9/4
-EI y' = -x^4/36 + 3x^2/4 - 9x/4 + A
-EI y = -x^5/180 + x^3/4 - 9 x^2/8 + Ax + B
Untuk potongan kedua perhatikan gambar di bawah ini :
3/2 ≤ x ≤ 3
qx = (3 - x)/(3/2) * 1
qx = 2(3 - x)/3
Mx = (Va)(x) - Ma - 1/2 * 1 * 3/2 * (x - 2/3 * 3/2) - qx * (x - 3/2) * (3/2 + (x - 3/2)/2) - 1/2 * (1 - qx)(x - 3/2) * 2/3 * (x - 3/2)
Mx = (3/2)(x) - 9/4 - 1/2 * 1 * 3/2 * (x - 2/3 * 3/2) - 2(3 - x)/3 * (x - 3/2) * (3/2 + (x - 3/2)/2) - 1/2 * (1 - 2(3 - x)/3)(x - 3/2) * 2/3 * (x - 3/2)
Mx = 1/18 * (2x^3 - 27x + 27)
periksa hasil Mx di atas sudah cocok dengan Mx dipotongan kedua,
M(3/2) = 1/18 * (2 (3/2)^3 - 27(3/2) + 27)
M(3/2) = -3/8 kNm
M(3) = 1/18 * (2 * 3^3 - 27 * 3 + 27)
M(3) = 0
OK cocok
penerapan persamaan euler-bernoulli,
-EI y'' = Mx
-EI y'' = 1/18 * (2x^3 - 27x + 27)
-EI y' = x^4/36 - 3x^2/4 + 3x/2 + C
-EI y = x^5/180 - x^3/4 + 3 x^2/4 + Cx + D
syarat batas dari potongan struktur pertama, 0 ≤ x ≤ 3/2
y(0) = y'(0) = 0
menghasilkan A = B = 0 sehingga persamaan masing-masing menjadi :
-EI y' = -x^4/36 + 3x^2/4 - 9x/4
-EI y = -x^5/180 + x^3/4 - 9 x^2/8
syarat batas dari potongan struktur kedua, 3/2 ≤ x ≤ 3
y'(3/2) potongan kedua = y'(3/2) potongan pertama
x^4/36 - 3x^2/4 + 3x/2 + C = -x^5/180 + x^3/4 - 9 x^2/8
(3/2)^4/36 - 3(3/2)^2/4 + 3(3/2)/2 + C = -(3/2)^4/36 + 3(3/2)^2/4 - 9(3/2)/4
C = -81/32
y(3/2) potongan kedua = y(3/2) potongan pertama
x^5/180 - x^3/4 + 3 x^2/4 + Cx + D = -x^5/180 + x^3/4 - 9 x^2/8
(3/2)^5/180 - (3/2)^3/4 + 3(3/2)^2/4 + (-81/32)(3/2) + D = -(3/2)^5/180 + (3/2)^3/4 - 9(3/2)^2/8
D = 189/160
sehingga persamaan putaran sudut dan deformasinya adalah
-EI y' = x^4/36 - 3x^2/4 + 3x/2 - 81/32
-EI y = x^5/180 - x^3/4 + 3 x^2/4 - 81x/32 + 189/160
untuk x = 3
-EI y' = 3^4/36 - 3 * 3^2/4 + 3 * 3/2 - 81/32
y' = θc = 81/(32EI)
-EI y = 3^5/180 - 3^3/4 + 3 * 3^2/4 - 81* 3/32 + 189/160
y = 81/(16EI)
maka lendutan di titik C adalah
δc = y + 1.75 y'
δc = 81/(16EI) + 1.75 * 81/(32EI)
δc = 1215/(128EI)
Analisis untuk struktur statis tertentu kedua
Va = Rc (arahnya ke bawah)
Ma = 4.75Rc (arahnya searah jarum jam)
Mx = Ma - (Va)(x)
Mx = 4.75Rc - (Rc)(x)
-EI y'' = Mx
-EI y'' = 4.75Rc - (Rc)(x)
-EI y' = 4.75Rc * x - (Rc)(x^2)/2 + c
-EI y = 4.75Rc/2 * x^2 - (Rc)(x^3)/6 + c * x + C
dengan syarat batas y'(0) = y(0) = 0 maka c = C = 0
persamaan putaran sudutnya :
-EI y' = 4.75Rc * x - (Rc)(x^2)/2
untuk x = 4.75
-EI y' = 4.75Rc * 4.75 - (Rc)(4.75^2)/2
y' = -361 Rc/(32EI)
persamaan kurvanya :
-EI y = 4.75Rc/2 * x^2 - (Rc)(x^3)/6
di x = 4.75
-EI y = 4.75Rc/2 * 4.75^2 - (Rc)(4.75^3)/6
y = -6859 Rc/(192EI)
Analisis untuk struktur statis tertentu ketiga
Va = 0
Ma = Mc (arahnya berlawanan arah jarum jam)
Mx = -Mc
-EI y'' = Mx
-EI y'' = -Mc
-EI y' = -Mc x + c
-EI y = -1/2 * Mc x^2 + c * x + C
dengan syarat batas y'(0) = y(0) = 0 maka c = C = 0
persamaan putaran sudutnya,
-EI y' = -Mc x
untuk x = 4.75
-EI y' = -Mc * 4.75
y' = 19 Mc/(4 EI)
persamaan kurvanya :
-EI y = -1/2 * Mc x^2
untuk x = 4.75
-EI y = -1/2 * Mc * 4.75^2
y = 361 Mc/(32EI)
dengan menerapkan syarat kesetimbangan di titik C,
Σ putaran sudut = 0
81/(32EI) + (-361 Rc/(32EI)) + 19 Mc/(4 EI) = 0. . . . . . . . . . . . . . (persamaan 1)
Σ perpindahan = 0
1215/(128EI) + -6859 Rc/(192EI) + 361 Mc/(32EI) = 0. . . . . . . . . . (persamaan 2)
diperoleh dua persamaan dalam dua variabel, Rc dan Mc, selesaikan sehingga diperoleh :
Rc = 2673/6859 kN
Mc = 567/1444 kNm
kemudian lihat struktur secara keseluruhan, sekarang permasalah statis tak tentu derajat 2 mejadi struktur statis tertentu.
ΣFy = 0
Va - 1/2 * 1 * 3 + Rc = 0
Va - 1/2 * 1 * 3 + 2673/6859 = 0
Va = 15231/13718 kN (arahnya ke atas)
ΣM di titik A = 0
-Ma + 1/2 * 1 * 3 * 3/2 - (Rc)(3 + 1.75) + Mc = 0
-Ma + 1/2 * 1 * 3 * 3/2 - (2673/6859)(3 + 1.75) + 567/1444 = 0
Ma = 1143/1444 kNm
periksa hasil di atas sudah benar atau masih salah,
ΣM di titik C = 0
(Va)(3 + 1.75) - Ma - 1/2 * 3 * 1 * (3/2 + 1.75) + Mc = 0
(15231/13718)(3 + 1.75) - 1143/1444 - 1/2 * 3 * 1 * (3/2 + 1.75) + 567/1444 = 0
0 = 0
Ok cocok
Udah diedit gambar dan keterangannya biar lebih jelas...
kita coba dengan contoh yang lain, perhatikan gambar di bawah ini,
akan dicari semua reaksi perletakannya, untuk itu struktur di atas termasuk statis tak tentu derajat 1, artinya terdapat 1 kelebihan gaya sehingga diagram superposisinya seperti di bawah ini :
untuk struktur statis tertentu yang pertama
mencari reaksi perletakan,
ΣM di A = 0
1/2 * q * (L/2)^2 + P * (L/2 + L/4) - (Vc)(L) = 0
Vc = 1/8 * (qL + 6P)
ΣFy = 0
Va + Vc - (q)(L/2) - P = 0
Va + 1/8 * (qL + 6P) - (q)(L/2) - P = 0
Va = 1/8 * (3 q L + 2P)
periksa reaksi di atas sudah benar ?
ΣM di C = 0
(Va)(L) - (q)(L/2)(3L/4) - (P)(L/4) = 0
1/8 * (3 q L + 2P) * (L) - (q)(L/2)(3L/4) - (P)(L/4) = 0
0 = 0
Ok cocok
interval 0 ≤ x ≤ L/2, perhatikan struktur di bawah ini :
persamaan momen gaya dalamnya adalah
0 ≤ x ≤ L/2
Mx = (Va)(x) - 1/2 * q * x^2
Mx = 1/8 * (3 q L + 2P) * (x) - 1/2 * q * x^2
Mx = 1/8 * (3 L q +2 P)x - q x^2/2
M(0) = 0
M(L/2) = 1/8 * (3 L q + 2 P)L/2 - q (L/2)^2/2
M(L/2) = L^2 q/16 + L P/8
M(L/2) harus sama dengan M(L/2) dari segmen selanjutnya,
penerapan persamaan euler-bernoulli,
-2EI y'' = Mx
-2EI y'' = 1/8 * (3 L q + 2 P)x - q x^2/2
-EI y' = 1/96 * x^2 (9 L q + 6 P - 8 q x) + A
-EI y = 1/96 * x^3 (3 L q + 2 (P - 2 q x)) + Ax + B
interval L/2 ≤ x ≤ 3L/4, perhatikan struktur di bawah ini :
Mx = (Va)(x) - (q)(L/2)(L/4 + x - L/2)
Mx = 1/8 * (3 q L + 2P)(x) - (q)(L/2)(L/4 + x - L/2)
Mx = L^2 q/8 - L q x/8 + P x/4
M(L/2) = L^2 q/8 - L q * (L/2)/8 + P * (L/2)/4
M(L/2) = L^2 q/16 + L P/8
ok udah cocok dengan M(L/2) segmen sebelumnya....
dilanjut nanti ya...
silakan buat agan/sist yang mau melanjutkan...
kita belajar bersama...
Spoiler for bahasan sebelumnya:
Quote:
bingungsetelah membaca posting sebelumnya :
Spoiler for bahasan sebelumnya:
sambil menunggu pertanyaan dari kaskusers, kita lanjutkan pembahasan kita.
Setelah mempelajari :
kita coba terapkan dasar teori yang sama untuk menyelesaikan struktur statis tak tentu. Prinsipnya sangat sederhana, dengan mengasumsikan kondisi struktur adalah linear elastik, maka analisis kita berlaku superposisi secara linear elastik juga, contoh:
karena struktur bersifat linear elastik, maka prinsip superposisi secara linear elastikpun berlaku. Artinya untuk kondisi struktur paling atas, bisa diuraikan tahapan analisisnya secara terpisah menjadi struktur tengah dan struktur paling bawah.
Nanti kita coba untuk beberapa permasalahan struktur statis tak tentu.
Silakan buat agan/sista yang mau berkontribusi/bertanya dll....ditunggu.
Setelah mempelajari :
- http://www.kaskus.co.id/show_post/53...208b47d4/370/-
- http://www.kaskus.co.id/show_post/53...328b45e1/371/-
- http://www.kaskus.co.id/show_post/53...6d8b4606/372/-
- http://www.kaskus.co.id/show_post/53...0d8b468a/373/-
- http://www.kaskus.co.id/show_post/53...2c8b45de/378/-
- http://www.kaskus.co.id/show_post/53...018b465a/379/-
- http://www.kaskus.co.id/show_post/53...758b4706/384/-
- http://www.kaskus.co.id/show_post/53...5b8b460b/391/-
kita coba terapkan dasar teori yang sama untuk menyelesaikan struktur statis tak tentu. Prinsipnya sangat sederhana, dengan mengasumsikan kondisi struktur adalah linear elastik, maka analisis kita berlaku superposisi secara linear elastik juga, contoh:
karena struktur bersifat linear elastik, maka prinsip superposisi secara linear elastikpun berlaku. Artinya untuk kondisi struktur paling atas, bisa diuraikan tahapan analisisnya secara terpisah menjadi struktur tengah dan struktur paling bawah.
- lihat struktur paling atas,
d = 2j - r - m
d = 2(3) - 4 - 1
d = 1
jadi struktur paling atas termasuk statis tak tentu derajat 1. Sehingga ada satu kelebihan gaya (redundant) yang harus dihilangkan untuk sementera sehingga strukturnya menjadi statis tertentu. Satu gaya redundant yang dipilih boleh yang mana saja, reaksi perletakan di A, di B atau di C. Untuk gambar di atas, dipilih reaksi perletakan di B sebagai gaya kelebihan.
- Setelah diperoleh struktur yang tengah, maka kita bisa lakukan perhitungan struktur statis tertentu seperti yang sudah kita bahas bersama. Dimulai dengan mencari reaksi perletakan Ra dan Rc, mencari gaya-gaya dalam, menerapkan persamaan Euler-Bernoulli dan mencari lendutan di titik B.
- Untuk struktur yang paling bawah, semua gaya luar sudah tidak ada, yang ada berupa gaya Rb (besarnya belum tahu dan dimisalkan arahnya ke atas) yang merupakan representasi dari gaya reaksi di perletakan B. Hitunglah reaksi perletakan di A dan C akibat gaya Rb, kemudian cari gaya-gaya dalamnya. Dilanjutkan dengan menerapkan persamaan Euler-Bernoulli untuk mendapatkan lendutan di titik B.
- Gunakan syarat kesetimbangan seperti yang sudah di bahas di http://www.kaskus.co.id/show_post/52...lisis-struktur
Σ gaya = 0. . . . . . . . . . . . . . .(persamaan ini sudah digunakan sebelumnya)
Σ perpindahan = 0. . . . . . . (persamaan ini digunakan untuk mencari gaya redundant)
karena kita sudah menghitung perpindahan di titik B berdasarkan struktur tengah (misalkan besarnya adalah d1) dan perpindahan di titik B berdasarkan struktru paling bawah (misalkan besarnya adalah d2), maka berdasarkan persamaan di atas,
Σ perpindahan = 0
δ1 + δ2 = 0
δ1 + f(Rb) = 0
δ2 adalah fungsi dari reaksi di B, Rb sehingga besar dan arah Rb bisa ditentukan. Jika Rb > 0 artinya arahnya pemisalan arah gaya Rb sudah benar, kalo Rb < 0 artinya pemisalan arah gaya Rb terbalik.
Nanti kita coba untuk beberapa permasalahan struktur statis tak tentu.
Silakan buat agan/sista yang mau berkontribusi/bertanya dll....ditunggu.
dan permintaan dari sista avalokitha,
Quote:
Original Posted By avalokitha►ayo gan TS .. dilanjut ke contoh soal struktur statis tak tentu, ane nyimak aja 
kita coba menjawab nomor 1 di atas, perhatikan gambar di bawah ini :
struktur di atas termasuk statis tak tentu derajat 2, oleh karena itu ada 2 redundant. TS pilih gaya reaksi di C Rc dan momen gaya di C Mc sebagai gaya kelebihan.
Analisis untuk struktur statis tertentu pertama
supaya gak bingung saat menganalisis struktur statis tertentu yang pertama, TS berikan ilustrasinya supaya lebih jelas. Untuk potongan pertama perhatikan gambar di bawah ini :
0 ≤ x ≤ 3/2
qx = x/(3/2) * 1
qx = 2x/3
Mx = (Va)(x) - Ma - 1/2 * x * qx * x/3
Mx = (3/2)(x) - 9/4 - 1/2 * x * 2x/3 * x/3
Mx = -x^3/9 + 3x/2 - 9/4
periksa :
M(0) = - 9/4 = Ma
M(3/2) = -(3/2)^3/9 + 3(3/2)/2 - 9/4
M(3/2) = -3/8 kNm
hasil Mx ini harus sama dengan Mx dari potongan kedua di bawah,
penerapan persamaan euler-bernoulli,
-EI y'' = -x^3/9 + 3x/2 - 9/4
-EI y' = -x^4/36 + 3x^2/4 - 9x/4 + A
-EI y = -x^5/180 + x^3/4 - 9 x^2/8 + Ax + B
Untuk potongan kedua perhatikan gambar di bawah ini :
3/2 ≤ x ≤ 3
qx = (3 - x)/(3/2) * 1
qx = 2(3 - x)/3
Mx = (Va)(x) - Ma - 1/2 * 1 * 3/2 * (x - 2/3 * 3/2) - qx * (x - 3/2) * (3/2 + (x - 3/2)/2) - 1/2 * (1 - qx)(x - 3/2) * 2/3 * (x - 3/2)
Mx = (3/2)(x) - 9/4 - 1/2 * 1 * 3/2 * (x - 2/3 * 3/2) - 2(3 - x)/3 * (x - 3/2) * (3/2 + (x - 3/2)/2) - 1/2 * (1 - 2(3 - x)/3)(x - 3/2) * 2/3 * (x - 3/2)
Mx = 1/18 * (2x^3 - 27x + 27)
periksa hasil Mx di atas sudah cocok dengan Mx dipotongan kedua,
M(3/2) = 1/18 * (2 (3/2)^3 - 27(3/2) + 27)
M(3/2) = -3/8 kNm
M(3) = 1/18 * (2 * 3^3 - 27 * 3 + 27)
M(3) = 0
OK cocok
penerapan persamaan euler-bernoulli,
-EI y'' = Mx
-EI y'' = 1/18 * (2x^3 - 27x + 27)
-EI y' = x^4/36 - 3x^2/4 + 3x/2 + C
-EI y = x^5/180 - x^3/4 + 3 x^2/4 + Cx + D
syarat batas dari potongan struktur pertama, 0 ≤ x ≤ 3/2
y(0) = y'(0) = 0
menghasilkan A = B = 0 sehingga persamaan masing-masing menjadi :
-EI y' = -x^4/36 + 3x^2/4 - 9x/4
-EI y = -x^5/180 + x^3/4 - 9 x^2/8
syarat batas dari potongan struktur kedua, 3/2 ≤ x ≤ 3
y'(3/2) potongan kedua = y'(3/2) potongan pertama
x^4/36 - 3x^2/4 + 3x/2 + C = -x^5/180 + x^3/4 - 9 x^2/8
(3/2)^4/36 - 3(3/2)^2/4 + 3(3/2)/2 + C = -(3/2)^4/36 + 3(3/2)^2/4 - 9(3/2)/4
C = -81/32
y(3/2) potongan kedua = y(3/2) potongan pertama
x^5/180 - x^3/4 + 3 x^2/4 + Cx + D = -x^5/180 + x^3/4 - 9 x^2/8
(3/2)^5/180 - (3/2)^3/4 + 3(3/2)^2/4 + (-81/32)(3/2) + D = -(3/2)^5/180 + (3/2)^3/4 - 9(3/2)^2/8
D = 189/160
sehingga persamaan putaran sudut dan deformasinya adalah
-EI y' = x^4/36 - 3x^2/4 + 3x/2 - 81/32
-EI y = x^5/180 - x^3/4 + 3 x^2/4 - 81x/32 + 189/160
untuk x = 3
-EI y' = 3^4/36 - 3 * 3^2/4 + 3 * 3/2 - 81/32
y' = θc = 81/(32EI)
-EI y = 3^5/180 - 3^3/4 + 3 * 3^2/4 - 81* 3/32 + 189/160
y = 81/(16EI)
maka lendutan di titik C adalah
δc = y + 1.75 y'
δc = 81/(16EI) + 1.75 * 81/(32EI)
δc = 1215/(128EI)
Analisis untuk struktur statis tertentu kedua
Va = Rc (arahnya ke bawah)
Ma = 4.75Rc (arahnya searah jarum jam)
Mx = Ma - (Va)(x)
Mx = 4.75Rc - (Rc)(x)
-EI y'' = Mx
-EI y'' = 4.75Rc - (Rc)(x)
-EI y' = 4.75Rc * x - (Rc)(x^2)/2 + c
-EI y = 4.75Rc/2 * x^2 - (Rc)(x^3)/6 + c * x + C
dengan syarat batas y'(0) = y(0) = 0 maka c = C = 0
persamaan putaran sudutnya :
-EI y' = 4.75Rc * x - (Rc)(x^2)/2
untuk x = 4.75
-EI y' = 4.75Rc * 4.75 - (Rc)(4.75^2)/2
y' = -361 Rc/(32EI)
persamaan kurvanya :
-EI y = 4.75Rc/2 * x^2 - (Rc)(x^3)/6
di x = 4.75
-EI y = 4.75Rc/2 * 4.75^2 - (Rc)(4.75^3)/6
y = -6859 Rc/(192EI)
Analisis untuk struktur statis tertentu ketiga
Va = 0
Ma = Mc (arahnya berlawanan arah jarum jam)
Mx = -Mc
-EI y'' = Mx
-EI y'' = -Mc
-EI y' = -Mc x + c
-EI y = -1/2 * Mc x^2 + c * x + C
dengan syarat batas y'(0) = y(0) = 0 maka c = C = 0
persamaan putaran sudutnya,
-EI y' = -Mc x
untuk x = 4.75
-EI y' = -Mc * 4.75
y' = 19 Mc/(4 EI)
persamaan kurvanya :
-EI y = -1/2 * Mc x^2
untuk x = 4.75
-EI y = -1/2 * Mc * 4.75^2
y = 361 Mc/(32EI)
dengan menerapkan syarat kesetimbangan di titik C,
Σ putaran sudut = 0
81/(32EI) + (-361 Rc/(32EI)) + 19 Mc/(4 EI) = 0. . . . . . . . . . . . . . (persamaan 1)
Σ perpindahan = 0
1215/(128EI) + -6859 Rc/(192EI) + 361 Mc/(32EI) = 0. . . . . . . . . . (persamaan 2)
diperoleh dua persamaan dalam dua variabel, Rc dan Mc, selesaikan sehingga diperoleh :
Rc = 2673/6859 kN
Mc = 567/1444 kNm
kemudian lihat struktur secara keseluruhan, sekarang permasalah statis tak tentu derajat 2 mejadi struktur statis tertentu.
ΣFy = 0
Va - 1/2 * 1 * 3 + Rc = 0
Va - 1/2 * 1 * 3 + 2673/6859 = 0
Va = 15231/13718 kN (arahnya ke atas)
ΣM di titik A = 0
-Ma + 1/2 * 1 * 3 * 3/2 - (Rc)(3 + 1.75) + Mc = 0
-Ma + 1/2 * 1 * 3 * 3/2 - (2673/6859)(3 + 1.75) + 567/1444 = 0
Ma = 1143/1444 kNm
periksa hasil di atas sudah benar atau masih salah,
ΣM di titik C = 0
(Va)(3 + 1.75) - Ma - 1/2 * 3 * 1 * (3/2 + 1.75) + Mc = 0
(15231/13718)(3 + 1.75) - 1143/1444 - 1/2 * 3 * 1 * (3/2 + 1.75) + 567/1444 = 0
0 = 0
Ok cocok
Udah diedit gambar dan keterangannya biar lebih jelas...
kita coba dengan contoh yang lain, perhatikan gambar di bawah ini,
akan dicari semua reaksi perletakannya, untuk itu struktur di atas termasuk statis tak tentu derajat 1, artinya terdapat 1 kelebihan gaya sehingga diagram superposisinya seperti di bawah ini :
untuk struktur statis tertentu yang pertama
mencari reaksi perletakan,
ΣM di A = 0
1/2 * q * (L/2)^2 + P * (L/2 + L/4) - (Vc)(L) = 0
Vc = 1/8 * (qL + 6P)
ΣFy = 0
Va + Vc - (q)(L/2) - P = 0
Va + 1/8 * (qL + 6P) - (q)(L/2) - P = 0
Va = 1/8 * (3 q L + 2P)
periksa reaksi di atas sudah benar ?
ΣM di C = 0
(Va)(L) - (q)(L/2)(3L/4) - (P)(L/4) = 0
1/8 * (3 q L + 2P) * (L) - (q)(L/2)(3L/4) - (P)(L/4) = 0
0 = 0
Ok cocok
interval 0 ≤ x ≤ L/2, perhatikan struktur di bawah ini :
persamaan momen gaya dalamnya adalah
0 ≤ x ≤ L/2
Mx = (Va)(x) - 1/2 * q * x^2
Mx = 1/8 * (3 q L + 2P) * (x) - 1/2 * q * x^2
Mx = 1/8 * (3 L q +2 P)x - q x^2/2
M(0) = 0
M(L/2) = 1/8 * (3 L q + 2 P)L/2 - q (L/2)^2/2
M(L/2) = L^2 q/16 + L P/8
M(L/2) harus sama dengan M(L/2) dari segmen selanjutnya,
penerapan persamaan euler-bernoulli,
-2EI y'' = Mx
-2EI y'' = 1/8 * (3 L q + 2 P)x - q x^2/2
-EI y' = 1/96 * x^2 (9 L q + 6 P - 8 q x) + A
-EI y = 1/96 * x^3 (3 L q + 2 (P - 2 q x)) + Ax + B
interval L/2 ≤ x ≤ 3L/4, perhatikan struktur di bawah ini :
Mx = (Va)(x) - (q)(L/2)(L/4 + x - L/2)
Mx = 1/8 * (3 q L + 2P)(x) - (q)(L/2)(L/4 + x - L/2)
Mx = L^2 q/8 - L q x/8 + P x/4
M(L/2) = L^2 q/8 - L q * (L/2)/8 + P * (L/2)/4
M(L/2) = L^2 q/16 + L P/8
ok udah cocok dengan M(L/2) segmen sebelumnya....
dilanjut nanti ya...
silakan buat agan/sist yang mau melanjutkan...
kita belajar bersama...
kita lanjutkan lagi...
penerapan persamaan euler-bernoulli pada segmen L/2 ≤ x ≤ 3L/4
-2EI y'' = Mx
-2EI y'' = L^2 q/8 - L q x/8 + P x/4
-EI y' = 1/16 * L^2 q x - 1/32 * L q x^2 + P x^2/16 + U
-EI y = 1/32 * L^2 q x^2 - 1/96 * L q x^3 + P x^3/48 + Ux + V
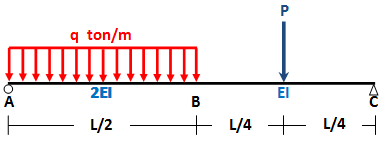
Selanjutnya untuk potongan sebelah kanan, lihat gambar di bawah ini,
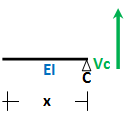
untuk 0 ≤ x ≤ L/4
Mx = (Vc)(x)
Mx = 1/8 * (q L + 6P)(x)
M(0) = 1/8 * (q L + 6P)(0) = 0
M(L/4) = 1/8 * (q L + 6P)(L/4)
M(L/4) = L^2 q/32 + 3 L P/16
M(L/4) harus sama dengan M(L/4) dari segmen lainnya,
penerapan persamaan euler-bernoulli,
EI y'' = Mx
EI y'' = 1/8 * (q L + 6P)(x)
EI y' = 1/16 * L q x^2 + 3 P x^2/8 + C
EI y = 1/48 * L q x^3 + P x^3/8 + Cx + D
untuk potongan selanjutnya, perhatikan gambar di bawah ini,
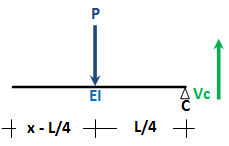
untuk L/4 ≤ x ≤ L/2
Mx = (Vc)(x) - (P)(x - L/4)
Mx = 1/8 * (q L + 6P)(x) - (P)(x - L/4)
Mx = L P/4 + L q x/8 - P x/4
M(L/4) = L P/4 + L q (L/4)/8 - P (L/4)/4
M(L/4) = L^2 q/32 + 3 L P/16
M(L/2) = L P/4 + L q (L/2)/8 - P (L/2)/4
M(L/2) = L^2 q/16 + L P/8
ok cocok dengan M(L/4) dan M(L/2) dari segmen sebelumnya,
penerapan persamaan euler-bernoulli,
-EI y'' = Mx
-EI y'' = L P/4 + L q x/8 - P x/4
-EI y' = L P x/4 + 1/16 * L q x^2 - P x^2/8 + R
-EI y = 1/8 * L P x^2 + 1/48 * L q x^3 - P x^3/24 + Rx + S
syarat batas yang dimiliki adalah
segmen AB 0 ≤ x ≤ L/2 dengan sebagian segmen CB L/4 ≤ x ≤ L/2
y(0) = 0
-EI y = 1/96 * x^3 (3 L q + 2 (P - 2 q x)) + Ax + B
0 = 1/96 * 0^3 (3 L q + 2 (P - 2 q * 0)) + A * 0 + B
B = 0
y'(L/2) segmen AB = y'(L/2) sebagian segmen BC
1/96 * x^2 (9 L q + 6 P - 8 q x) + A = 1/16 * L^2 q x - 1/32 * L q x^2 + P x^2/16 + U
1/96 * (L/2)^2 (9 L q + 6 P - 8 q * (L/2)) + A = 1/16 * L^2 q * (L/2) - 1/32 * L q (L/2)^2 + P (L/2)^2/16 + U. . . . . . . . . . . . . . . (persamaan 1)
y(L/2) segmen AB = y(L/2) sebagian segmen BC
1/96 * x^3 (3 L q + 2 (P - 2 q x)) + Ax = 1/32 * L^2 q x^2 - 1/96 * L q x^3 + P x^3/48 + Ux + V
1/96 * (L/2)^3 (3 L q + 2 (P - 2 q * (L/2))) + A * (L/2) = 1/32 * L^2 q * (L/2)^2 - 1/96 * L q * (L/2)^3 + P (L/2)^3/48 + U * (L/2) + V. . . . . . . . . . . . . . . (persamaan 2)
baru terbentuk 2 persamaan...
nanti dilanjut lagi....
hasil di atas belum tentu benar...
nanti di cek lagi...
silakan agan/sist mau ikutan periksa lagi atau sekaligus menyelesaikannya...
ditunggu...
0