kalau besar, tipe dan posisi gaya serta jumlah perletakan berubah, maka analisisnya juga berubah. Namun prinsipnya sama saja.



boleh dong...
kirim saja ke tasik11111@yahoo.com



sel = selisih dari (Mtotal - FEM)

setsel = setengah selisih = mencari CO (carry over)

msetsel = minus dari setsel = -setsel

jumlah = sel + msetsel

gaya = gaya reaksi di perletakan akbat Mtotal dan beban eksternal.

besar sudut tetha di perletakan = jumlah/(3EI/L)



perhatikan gambar di bawah ini untuk mencari gaya reaksi Vi dan Vj



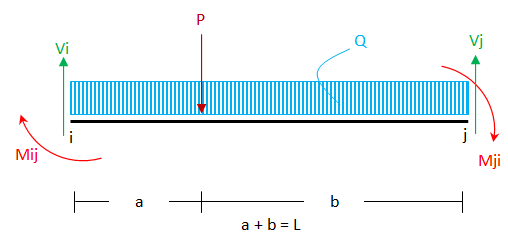
ΣM di titik j = 0

Mij + Mji + Vi * L - P * b - ½ Q L² = 0

Vi = -(Mij + Mji - P * b - ½ Q L²)/L


dengan cara yang sama untuk ΣM di titik i = 0

Vj = (Mij + Mji + P * a + ½ Q L²)/L


jika hanya ada beban terbagi rata Q = 1 dan L = 1 maka :

Vi = -(Mij + Mji - ½ * 1 * 1²)/1

Vj = (Mij + Mji + ½ * 1 * 1²)/1



dan untuk mencari momen gaya di lapangan, perhatikan potongan struktur di bawah ini :



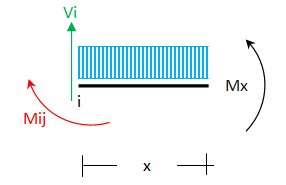
berdasarkan syarat kesetimbangan,

ΣM di potongan = 0

-Mx - ½ Q x² + Mij + Vi * x = 0

Mx = - ½ Q x² + Mij + Vi * x

jika hanya ada beban terbagi rata Q = 1 dan L = 1 maka momen gaya di tengah bentang, x = ½

Mx = - ½ * 1 * (½)² + Mij + ((Mij + Mji + ½ * 1 * 1²)/1) * ½

Mx bisa dicari.


demikian juga dengan cara yang sama untuk beban terpusat P = 1 ketika mencari reaksi perletakan Vi dan Vj serta momen gaya di tengah bentang.