ok...
program portal 3 susun sudah selesai dibuat, tapi akan posting nanti kalo ada permintaan khusus.
sekarang biar pembahasannya terstruktur rapi, kita lanjutkan dulu bahasan tentang metoda elastisitas. Akan kita pelajari struktur pembebanan seperti di bawah ini :



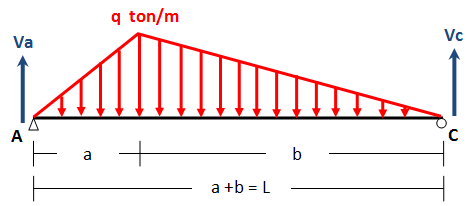
akan dicari putaran sudut di A dan C, posisi dan besar lendutan maksimum serta sketsa kurva elastis. Maka langkah penyelesaiannya adalah :

(a).

mencari reaksi perletakan,

ΣM di titik C = 0

(Va)(L) - 1/2 * a * q * (a/3 + b) - 1/2 * b * q * 2b/3 = 0

Va = q (a^2 + 3 a b + 2 b^2)/(6 L)



ΣFy = 0

Va + Vc - 1/2 * q * L = 0

q (a^2 + 3 a b + 2 b^2)/(6 L) + Vc - 1/2 * q * L = 0

Vc = q (-a^2 - 3 a b - 2 b^2 + 3 L^2)/(6 L)



(b).

memeriksa hasil yang diperoleh pada langkah (a),

ΣM di titik A = 0

1/2 * a * q * 2a/3 + 1/2 * b * q * (a + b/3) - (Vc)(L) = 0

1/2 * a * q * 2a/3 + 1/2 * b * q * (a + b/3) - (q (-a^2 - 3 a b - 2 b^2 + 3 L^2)/(6 L))(L) = 0

1/2 q (a + b - L) (a + b + L) = 0

karena L = a + b maka

1/2 q (L - L) (a + b + L) = 0

0 = 0

OK cocok



ΣM di puncak beban segitiga = 0

(Va)(a) - 1/2 * a * q * a/3 + 1/2 * b * q * b/3 - (Vc)(b) = 0

(q (a^2 + 3 a b + 2 b^2)/(6 L))(a) - 1/2 * a * q * a/3 + 1/2 * b * q * b/3 - (q (-a^2 - 3 a b - 2 b^2 + 3 L^2)/(6 L))(b) = 0

q (a + b - L)(a^2 + 3 a b + b (2 b+3 L))/L = 0

karena a + b = L maka

q (L - L)(a^2 + 3 a b + b (2 b+3 L))/L = 0

0 = 0

ok cocok



(c).

menghitung momen gaya internal Mx, lihat potongan struktur sebelah kiri di bawah ini :



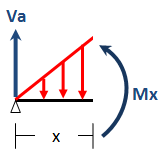
ΣM dipotongan = 0

(Va)(x) - 1/2 * x * x/a * q * x/3 - Mx = 0

Mx = (Va)(x) - 1/2 * x * x/a * q * x/3

Mx = (q (a^2 + 3 a b + 2 b^2)/(6 L))(x) - 1/2 * x * x/a * q * x/3

Mx = q x (a^3 + 3 a^2 b + 2 a b^2 - L x^2)/(6 a L)

ingat : L = (a + b) sehingga bentuk di atas menjadi,

Mx = q x (a^3 + 3 a^2 b + 2 a b^2 - (a + b) x^2)/(6 a L)

Mx = q x (a^2 + 2 a b - x^2)/(6 a)


dan perhatikan potongan struktur bagian kanan seperti terlihat pada gambar berikut :



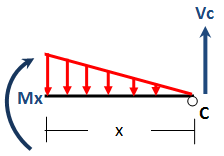
ΣM dipotongan = 0

Mx + 1/2 * x * x/b * q * x/3 - (Vc)(x) = 0

Mx = -1/2 * x * x/b * q * x/3 + (Vc)(x)

Mx = -1/2 * x * x/b * q * x/3 + (q (-a^2 - 3 a b - 2 b^2 + 3 L^2)/(6 L))(x)

Mx = q x (-a^2 b - 3 a b^2 - 2 b^3 + 3 b L^2 - L x^2)/(6 b L)

ingat : L = (a + b) sehingga bentuk di atas menjadi,

Mx = q x (a + b) (2 a b + b^2 - x^2)/(6 b L)

Mx = q x (2 a b + b^2 - x^2)/(6 b)






(d).

memeriksa, apakah Mx yang diperoleh pada langkah (c) sudah benar atau masih salah.

potongan kiri,

x = 0

Mx = q x (a^2 + 2 a b - x^2)/(6 a)

Mx = q * 0 * (a^2 + 2 a b - x^2)/(6 a)

Mx = 0

OK



x = a

Mx = q x (a^2 + 2 a b - x^2)/(6 a)

Mx = q * a * (a^2 + 2 a b - a^2)/(6 a)

Mx = a b q/3



untuk potongan kanan,

x = 0

Mx = q x (2 a b + b^2 - x^2)/(6 b)

Mx = q * 0 * (2 a b + b^2 - x^2)/(6 b)

Mx = 0

Ok cocok



x = b

Mx = q x (2 a b + b^2 - x^2)/(6 b)

Mx = q * b * (2 a b + b^2 - b^2)/(6 b)

Mx = a b q/3

(ok cocok dengan potongan kiri)



(e).

menerapkan persamaan Euler-Bernoulli,

potongan sebelah kiri,

-EI y'' = Mx

-EI y'' = q x (a^2 + 2 a b - x^2)/(6 a)

-EI y' = -q x^2 (-2 a^2 - 4 a b + x^2)/(24 a) + A

-EI y = q x^3 (10 a^2 + 20 a b - 3 x^2)/(360 a) + Ax + B



untuk potongan sebelah kanan,

-EI y'' = Mx

-EI y'' = q x (2 a b + b^2 - x^2)/(6 b)

-EI y' = q x^2 (4 a b + 2 b^2 - x^2)/(24 b) + C

-EI y = q x^3 (20 a b + 10 b^2 - 3 x^2)/(360 b) + Cx + D



(f).

memasukkan syarat batas,
deformasi pada potongan sebelah kiri,

y(0) = 0

-EI y = q x^3 (10 a^2 + 20 a b - 3 x^2)/(360 a) + Ax + B

0 = q * 0^3 (10 a^2 + 20 a b - 3 * 0^2)/(360 a) + A * 0 + B

B = 0


deformasi pada potongan sebelah kanan,

y(0) = 0

-EI y = q x^3 (20 a b + 10 b^2 - 3 x^2)/(360 b) + Cx + D

0 = q * 0^3 (20 a b + 10 b^2 - 3 * 0^2)/(360 b) + C * 0 + D

D = 0


meninjau putaran sudut dan lendutan,

y'(a)_potongan kiri = -y'(b)_potongan kanan

-q x^2 (-2 a^2 - 4 a b + x^2)/(24 a) + A = -(q x^2 (4 a b + 2 b^2 - x^2)/(24 b) + C)

-q a^2 (-2 a^2 - 4 a b + a^2)/(24 a) + A = -(q b^2 (4 a b + 2 b^2 - b^2)/(24 b) + C). . . . . . . . . . . . . . . . . . (persamaan 1)

q x^3 (10 a^2 + 20 a b - 3 x^2)/(360 a) + Ax + B = q x^3 (20 a b + 10 b^2 - 3 x^2)/(360 b) + Cx + D

q a^3 (10 a^2 + 20 a b - 3 a^2)/(360 a) + A * a + 0 = q b^3 (20 a b + 10 b^2 - 3 b^2)/(360 b) + C * b + 0. . . . . . . . . . . . . . . . . . (persamaan 2)

selesaikan dua persamaan dengan dua peubah A dan C sehingga menghasilkan :

A = (-1/360) q (7 a^3 + 28 a^2 b + 32 a b^2 + 8 b^3)

C = (-1/360) q (8 a^3 + 32 a^2 b + 28 a b^2 + 7 b^3)

sehingga solusi persamaan diferensialnya adalah :

potongan sebelah kiri,

-EI y' = -q x^2 (-2 a^2 - 4 a b + x^2)/(24 a) + A

-EI y = q x^3 (10 a^2 + 20 a b - 3 x^2)/(360 a) + Ax



untuk potongan sebelah kanan,

-EI y' = q x^2 (4 a b + 2 b^2 - x^2)/(24 b) + C

-EI y = q x^3 (20 a b + 10 b^2 - 3 x^2)/(360 b) + Cx

dalam hal ini C dan D adalah konstanta bilangan real yang sudah ditunjukkan di atas.

Maka putaran sudut di titik A adalah,

-EI y' = -q x^2 (-2 a^2 - 4 a b + x^2)/(24 a) + A

-EI y' = -q * 0^2 (-2 a^2 - 4 a b + 0^2)/(24 a) + A

-EI y' = A

-EI y' = (-1/360) q (7 a^3 + 28 a^2 b + 32 a b^2 + 8 b^3)

y' = 1/(360EI) q (7 a^3 + 28 a^2 b + 32 a b^2 + 8 b^3)


dengan cara yang sama, putara sudut di titik C adalah :

-EI y' = q x^2 (4 a b + 2 b^2 - x^2)/(24 b) + C

-EI y' = q * 0^2 (4 a b + 2 b^2 - 0^2)/(24 b) + C

-EI y' = C

-EI y' = (-1/360) q (8 a^3 + 32 a^2 b + 28 a b^2 + 7 b^3)

y' = 1/(360EI) q (8 a^3 + 32 a^2 b + 28 a b^2 + 7 b^3)


mencari lendutan maksimum, untuk menyederhanakan perhitungan tanpa hitung coba-coba, pasti lokasinya terletak di potongan kedua (kenapa ?)

-EI y' = q x^2 (4 a b + 2 b^2 - x^2)/(24 b) + C = 0

dalam hal ini C = (-1/360) q (8 a^3 + 32 a^2 b + 28 a b^2 + 7 b^3)

xbisa dicari dengan metoda numerik, sehingga lendutan maksimumnya bisa dihitung dengan mamasukkan ke persamaan lendutan potongan struktur sebelah kanan,

-EI y = q x^3 (20 a b + 10 b^2 - 3 x^2)/(360 b) + Cx

y bisa dihitung setelah x diketahui.




(g).

memeriksa hasil yang diperoleh pada langkah (f) sudah benar atau masih salah.

periksa putaran sudut di titik x = a bagian kiri,

-EI y' = -q x^2 (-2 a^2 - 4 a b + x^2)/(24 a) + A

-EI y' = -q a^2 (-2 a^2 - 4 a b + a^2)/(24 a) + A

-EI y' = (a^3 q)/24 + 1/6 a^2 b q + (-1/360) q (7 a^3 + 28 a^2 b + 32 a b^2 + 8 b^3)

-EI y' = 1/45 q (a^3 + 4 a^2 b - 4 a b^2 - b^3)


periksa putaran sudut di titik x = b bagian kanan,

-EI y' = q x^2 (4 a b + 2 b^2 - x^2)/(24 b) + C

-EI y' = q b^2 (4 a b + 2 b^2 - b^2)/(24 b) + C

-EI y' = 1/24 b q (4 a b + b^2) + (-1/360) q (8 a^3 + 32 a^2 b + 28 a b^2 + 7 b^3)

-EI y' = 1/45 q (-a^3 - 4 a^2 b + 4 a b^2 + b^3)

terlihat bahwa θ kiri = - θ kanan

OK cocok



periksa untuk lendutan x = a bagian kiri,

-EI y = q x^3 (10 a^2 + 20 a b - 3 x^2)/(360 a) + Ax

-EI y = q a^3 (10 a^2 + 20 a b - 3 a^2)/(360 a) + (-1/360) q (7 a^3 + 28 a^2 b + 32 a b^2 + 8 b^3) * a

-EI y = (1/45) a b q (-a^2 - 4 a b - b^2)



periksa untuk lendutan x = b bagian kanan,

-EI y = q x^3 (20 a b + 10 b^2 - 3 x^2)/(360 b) + Cx

-EI y = q b^3 (20 a b + 10 b^2 - 3 b^2)/(360 b) + (-1/360) q (8 a^3 + 32 a^2 b + 28 a b^2 + 7 b^3) * b

-EI y = (1/45) a b q (-a^2 - 4 a b - b^2)

terlihat bahwa Δ kiri = Δ kanan

OK cocok




(h).

sketsa kurva elastisnya berwarna hijau seperti terlihat pada gambar di bawah ini,



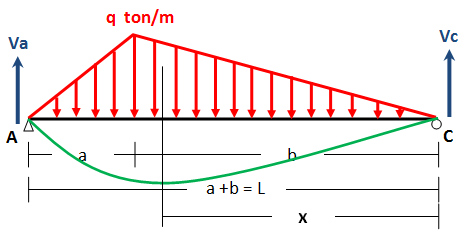
xadalah posisi lendutan maksimum dihitung dari titik C

Silakan buat agan/sist yang mau bertanya, punya usul, atau turut berkontribusi....ditunggu diskusinya...