metoda titik kumpul pernah diberikan di http://www.kaskus.co.id/thread/5271f...sis-struktur/3 post #56

dan metoda potongan atau ritter sudah dibahas di http://www.kaskus.co.id/thread/5271f...sis-struktur/6 post #120

untuk menjawab soal dari ibu emma, kita coba separuhnya dikerjakan dengan metoda titik kumpul, dan sisanya dengan metoda potongan.

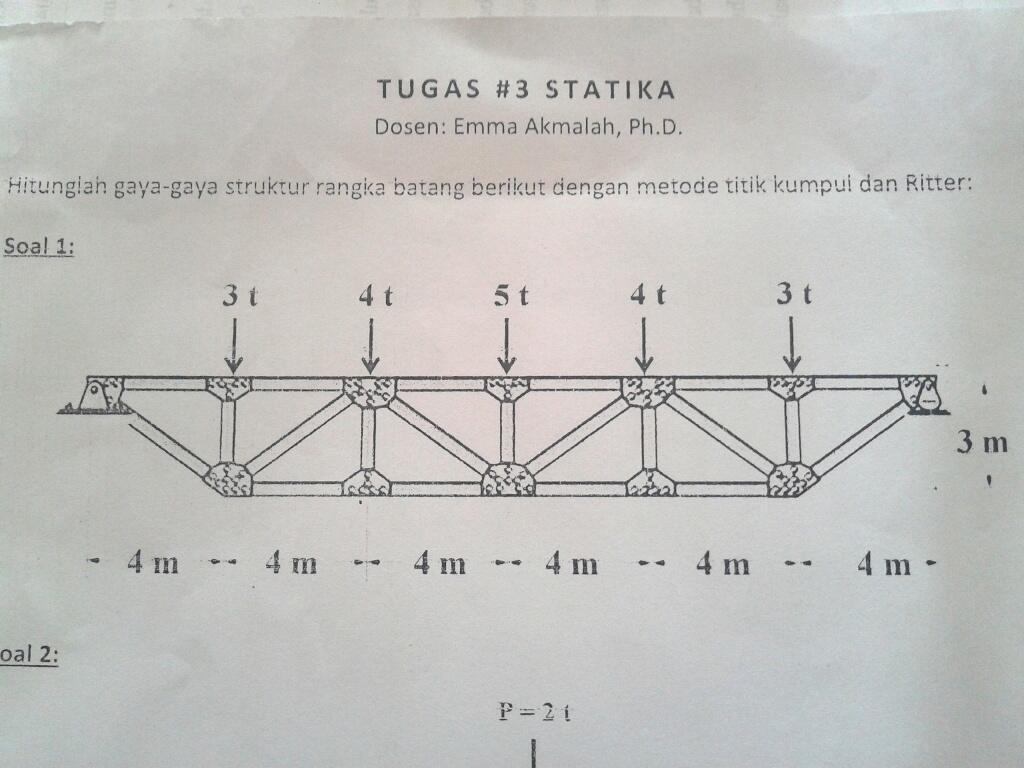
lihat gambar di bawah ini,



mencari reaksi perletakan di titik A, yaitu Ha dan Va kemudian reaksi perletakkan di G yaitu Vg

ΣM di titik G = 0

(Va)(6 * 4) - (3)(5 * 4) - (4)(4 * 4) - (5)(3 * 4) - (4)(2 * 4) - (3)(4) = 0

Va = 9.5 ton


ΣM di titik A = 0

(-Vg)(6 * 4) + (3)( 5 * 4) + (4)(4 * 4) + (5)(3 * 4) + (4)(2 * 4) + (3)(4) = 0

Vg = 9.5 ton


ΣFx = 0

Ha = 0



periksa reaksi perletakan di atas,

ΣFy = 0

Va + Vg - 3 - 4 - 5 - 4 - 3 = 0

9.5 + 9.5 - 3 - 4 - 5 - 4 - 3 = 0

0 = 0

Ok cocok....


harap diperhatikan, karena geometri jembatan dan pembebanannya adalah simetris, maka pastilah batang-batang yang simetris terhadap garis tengah jembatan akan menghasilkan gaya batang yang sama.





untuk mencari gaya-gaya batangnya lakukan analisis titik kumpul dan lihat gambar berikut,



sin Φ = 3/5

cos Φ = 4/5


Titik A,

ΣFy = 0

Va - N7 * (3/5) = 0

9.5 - N7 * (3/5) = 0

N7 = 15.8333 ton (tarik)


ΣFx = 0

N1 + N7 * 4/5 = 0

N1 + 15.8333 * 4/5 = 0

N1 = -12.6666 ton (tekan)





Titik B,

ΣFy = 0

-3 - N8 = 0

N8 = -3 ton (tekan)


ΣFx = 0

-N1 + N2 = 0

-(-12.6666 ) + N2 = 0

N2 = -12.6666 ton (tekan)




Titik H,

ΣFy = 0

N7 * 3/5 + N8 + N9 * 3/5 = 0

15.8333 * 3/5 + (-3) + N9 * 3/5 = 0

N9 = -10.8333 ton (tekan)


ΣFx = 0

-N7 * 4/5 + N9 * 4/5 + N18 = 0

-15.8333* 4/5 + (-10.8333) * 4/5 + N18 = 0

N18 = 21.3333 ton (tarik)





Titik I,

ΣFy = 0

N10 = 0


ΣFx = 0

N19 - N18 = 0

N19 = N18 = 21.3333 ton (tarik)




Titik C,

ΣFy = 0

-4 - N9 * 3/5 - N10 - N11 * 3/5 = 0

-4 - (-10.8333) * 3/5 - 0 - N11 * 3/5 = 0

N11 = 4.16663 ton (tarik)


ΣFx = 0

-N2 - N9 * 4/5 + N11 * 4/5 + N3 = 0

-(-12.6666) - (-10.8333) * 4/5 + 4.16663 * 4/5 + N3 = 0

N3 = -24.6665 ton (tekan)




Titik D,

ΣFy = 0

-5 - N12 = 0

N12 = -5 ton (tekan)


ΣFx = 0

-N3 + N4 = 0

-(-24.6665) + N4 = 0

N4 = -24.6665 ton (tekan)





Titik J,

ΣFy = 0

N11 * 3/5 + N12 + N13 * 3/5 = 0

4.16663 * 3/5 + (-5) + N13 * 3/5 = 0

N13 = 4.1667 ton (tarik)


ΣFx = 0

-N19 - N11 * 4/5 + N13 * 4/5 + N20 = 0

-21.3333 - 4.16663 * 4/5 + 4.1667 * 4/5 + N20 = 0

N20 = 21.3332 ton (tarik)




gaya-gaya batang lainnya simetris terhadap batang-batang yang sudah dihitung di atas....
sekarang periksa hasil di atas dengang metoda potongan atau ritter,
perhatikan gambar di bawah ini,



ΣM di C = 0

(-N18)(3) - (3)(4) + (Va)(2 * 4) = 0

(-N18)(3) - (3)(4) + (9.5)(2 * 4) = 0

N18 = 21.3333 ton (tarik)Cocok !



ΣM di H = 0

(N2)(3) + (Va)(4) = 0

(N2)(3) + (9.5)(4) = 0

N2 = -12.6667 ton (tekan) Cocok !


ΣFy = 0

N9 * (3/5) + Va - 3 = 0

N9 * (3/5) + 9.5 - 3 = 0

N9 = -10.8333 ton (tekan) Cocok !



selanjutnya lihat potonga struktur di bawah ini,



ΣM di C = 0

(-N19)(3) - (3)(4) + (Va)(2 * 4) = 0

(-N19)(3) - (3)(4) + (9.5)(2 * 4) = 0

N19 = 21.3333 ton (tarik) Cocok !


ΣFy = 0

Va - 3 + N9 * 3/5 + N10 = 0

9.5 - 3 + (-10.8333) * 3/5 + N10 = 0

N10 = 0 Ok Cocok !



kemudian lihat potongan struktur berikut ini,



ΣM di J = 0

(N3)(3) - (4)(4) - (3)(2 * 4) + (Va)(3 * 4) = 0

(N3)(3) - (4)(4) - (3)(2 * 4) + (9.5)(3 * 4) = 0

N3 = -24.6667 ton (tekan) Ok cocok !



ΣFx = 0

N3 + N11 * 4/5 + N19 = 0

-24.6667 + N11 * 4/5 + 21.3333 = 0

N11 = 4.16675 ton (tarik) Cocok !






gaya-gaya lainnya besarnya sama untuk elemen yang simetris terhadap sumbu tengah jembatan...