- Beranda
- The Lounge
Teori Matematika Ajaib Yang WOW :D
...
TS
forderation
Teori Matematika Ajaib Yang WOW :D
Quote:
Budayakan Comment Bermutu 
dan Rate 5 
dan Rate 5 
Quote:
Thanks for Mimin and Momod akhirnya HT Pertama Ane 
Quote:
Selama ane menjelajahi dunia Matematika, banyak hal-hal ajaib. Yang ane maksud ajaib adalah hal-hal yang aneh 
, mencenggangkan, mengherankan, dianggap mustahil bahkan bertentangan dengan akal sehat. Okey tanpa banyak basa-basi ini 10 hal ajaib di Matematika
, mencenggangkan, mengherankan, dianggap mustahil bahkan bertentangan dengan akal sehat. Okey tanpa banyak basa-basi ini 10 hal ajaib di MatematikaQuote:
Semoga kagak repsol
Spoiler for :
Quote:
10. 0,9999999…. = 1
ente ente pasti berpikir bahwa 0,9999999…. dan 1 adalah dua bilangan yang berbeda
. Tidak-tidak keduanya merupakan bilangan yang sama 
ente ente pasti berpikir bahwa 0,9999999…. dan 1 adalah dua bilangan yang berbeda
. Tidak-tidak keduanya merupakan bilangan yang sama
Spoiler for Penjelasan:
Penjelasan:
Salah satu alasan mengapa desimal tak terhingga merupakan perluasan yang perlu dari desimal terhingga adalah untuk merepresentasikan pecahan. Dengan menggunakan pembagian panjang, pembagian bilangan bulat yang sederhana seperti 1⁄3 akan menghasilkan desimal berulang 0,333…. Desimal berulang ini mempunyai digit yang berulang tanpa akhir. Desimal ini memberikan bukti cepat 0,999… = 1. Perkalian 3 kali 3 menghasilkan 9 pada setiap digit, sehingga 3 × 0,333… sama dengan 0,999…. Dan 3 × 1⁄3 sama dengan 1, sehingga 0,999… = 1.[1]
Bentuk pembuktian lainya adalah perkalian 1/9 = 0.111… dengan 9.
dan 
Salah satu alasan mengapa desimal tak terhingga merupakan perluasan yang perlu dari desimal terhingga adalah untuk merepresentasikan pecahan. Dengan menggunakan pembagian panjang, pembagian bilangan bulat yang sederhana seperti 1⁄3 akan menghasilkan desimal berulang 0,333…. Desimal berulang ini mempunyai digit yang berulang tanpa akhir. Desimal ini memberikan bukti cepat 0,999… = 1. Perkalian 3 kali 3 menghasilkan 9 pada setiap digit, sehingga 3 × 0,333… sama dengan 0,999…. Dan 3 × 1⁄3 sama dengan 1, sehingga 0,999… = 1.[1]
Bentuk pembuktian lainya adalah perkalian 1/9 = 0.111… dengan 9.
dan Quote:
9. Identitas Euler
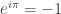
Jika agan lihat nilai e=2,71828182845904523536… , π = 3,14159265358979323846 dan i=√-1, sepertinya mustahil e pangkat iπ hasilnya -1
Pembuktian:
Nah, sekarang gw bakal ngebuktiin persamaan tersebut bener. ambil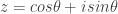
persamaan di bilangan complex lalu kita turunin diperoleh 
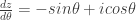Padahal 
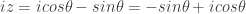inget 
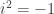jadi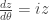 
,
,
,
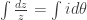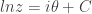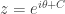Sekarang kita nyari nilai konstanta C karena z=cos\theta+isin\theta nilainya satu untuk \theta=0 maka nilai C adalah nol. Maka persamaan kita menjadi 
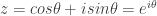Yang disebut dengan persamaan euler.Nah sekarang kita ambil nilai\theta=\pi diproleh 
= 
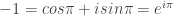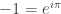Dan akhirnya kita dapet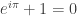 
Jika agan lihat nilai e=2,71828182845904523536… , π = 3,14159265358979323846 dan i=√-1, sepertinya mustahil e pangkat iπ hasilnya -1
Pembuktian:
Nah, sekarang gw bakal ngebuktiin persamaan tersebut bener. ambil
persamaan di bilangan complex lalu kita turunin diperoleh Padahal inget jadi ,,, Sekarang kita nyari nilai konstanta C karena z=cos\theta+isin\theta nilainya satu untuk \theta=0 maka nilai C adalah nol. Maka persamaan kita menjadi Yang disebut dengan persamaan euler.Nah sekarang kita ambil nilai\theta=\pi diproleh = Dan akhirnya kita dapet
Quote:
8. i pangkat i
Agan tahu bahwa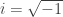
adalah bilangan imajiner, tapi apakah ente tahu i pangkat i hasilnya adalah bilangan real 
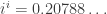. aneh bukan ? ane juga bingung kok gan 
Penjelasan:
Untuk mengetahuinya kita menggunakan persamaan euler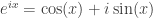
masukkan 
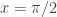diperoleh 
=
=
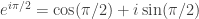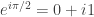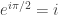Lalu pangkatkan kedua sisi dengan i diperoleh 
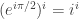karena sifat perpangkat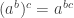an 
dan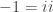 
diperoleh 
=
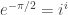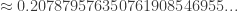dan i^i adalah bilangan transendental
Agan tahu bahwa
adalah bilangan imajiner, tapi apakah ente tahu i pangkat i hasilnya adalah bilangan real . aneh bukan ? ane juga bingung kok gan Penjelasan:
Untuk mengetahuinya kita menggunakan persamaan euler
masukkan diperoleh == Lalu pangkatkan kedua sisi dengan i diperoleh karena sifat perpangkatan dan diperoleh = dan i^i adalah bilangan transendentalQuote:
7. Jumlah sudut Segitiga tidak selalu 180°
Di Sekolah ente ente pasti diajarkan bahwa jumlah sudut segitiga adalah 180° (yaiyah dong gan
) , padahal sebenarnya jumlah sudut Segitiga tidak selalu 180°. Jumlah sudut segitiga tergantung pada bidang apa segitiga itu digambar. Jika segitiga itu digambar di bidang datar (Geometri Euclid) maka jumlah sudutnya selalu 180°. Akan tetapi jika segitiga terbut digambar di bidang cembung /cekung (Geometri Non-Euclid) maka jumlah sudutnya tidak lagi 180°. Okey gampangnya gini dech, coba ente gambar segitiga pada bola, lalu hitung sudutnya. Apa jumlahnya masih 180° 
?
Di Sekolah ente ente pasti diajarkan bahwa jumlah sudut segitiga adalah 180° (yaiyah dong gan
) , padahal sebenarnya jumlah sudut Segitiga tidak selalu 180°. Jumlah sudut segitiga tergantung pada bidang apa segitiga itu digambar. Jika segitiga itu digambar di bidang datar (Geometri Euclid) maka jumlah sudutnya selalu 180°. Akan tetapi jika segitiga terbut digambar di bidang cembung /cekung (Geometri Non-Euclid) maka jumlah sudutnya tidak lagi 180°. Okey gampangnya gini dech, coba ente gambar segitiga pada bola, lalu hitung sudutnya. Apa jumlahnya masih 180° ?Quote:
6. Himpunan tak-hingga
Sesuai namanya himpunan tak hingga adalah himpunan yang mempunyai tak-hingga elemen , bagaimana mengetahui sutu himpunan adalah tak-hingga atau bukan?
Definsi: Himpunan X dikatakan tak hingga jika terdapat X himpunan bagian yang sebenarnya (proper subset) S\subset X, sedemikian hingga X dan S mempunyai elemen yang sama banyaknya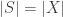
Contoh: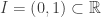
(himpunan bilangan real), tentunya agan tahu bahwa interval terbuka dari nol sampai satu bagian dari himpunan bilangan real akan tetapi apakah agan tahu bahwa I mempunyai elemen yang sama banyaknya dengan 
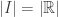? Mm..sepertinya suatu hal yang mustahil ya kan 
?
Sesuai namanya himpunan tak hingga adalah himpunan yang mempunyai tak-hingga elemen , bagaimana mengetahui sutu himpunan adalah tak-hingga atau bukan?
Definsi: Himpunan X dikatakan tak hingga jika terdapat X himpunan bagian yang sebenarnya (proper subset) S\subset X, sedemikian hingga X dan S mempunyai elemen yang sama banyaknya
Contoh:
(himpunan bilangan real), tentunya agan tahu bahwa interval terbuka dari nol sampai satu bagian dari himpunan bilangan real akan tetapi apakah agan tahu bahwa I mempunyai elemen yang sama banyaknya dengan ? Mm..sepertinya suatu hal yang mustahil ya kan ?Quote:
5. Teorema Fundamental Kalkulus
Turunan dan Integral adalah dua hal yang amat-amat berbeda. Akan tetapi Teorema Fundamental Kalkulus dapat menghubungkan kedua hal yang berbeda tersebut dengan amat cantiknya. Menurut Teorema Fundamental kalkulus: Integral merupakan anti turunan. Bagi ane, ini merupakan teorema terfavorit ane
.
Turunan dan Integral adalah dua hal yang amat-amat berbeda. Akan tetapi Teorema Fundamental Kalkulus dapat menghubungkan kedua hal yang berbeda tersebut dengan amat cantiknya. Menurut Teorema Fundamental kalkulus: Integral merupakan anti turunan. Bagi ane, ini merupakan teorema terfavorit ane
.Quote:
4. Grigori Perelman
Yup ini nama orang, nama matematikawan Rusia. Kenapa ane masukkan kedaftar ? Karena dia menolak 1 juta US Dollar atas jasanya memecahkan dugaan Poincare (kasih ke TS aja klo gk mau). Hanya orang gila atau luar biasa jenius yang menolak uang sebesar itu. 
Grisha Perelman, adalah seorang matematikawan Rusia berdarah Yahudi, yang membuat kontribusi terkenal kepada Geometri Riemannian dan topologi geometri. Khususnya, dia tampaknya telah membuktikan geometrisasi konjektur Thurston. Bila demikian, ini juga menyelesaikan konjektur Poincaré yang terkenal, yang dikeluarkan pada 1904 dan dianggap sebagai masalah terbuka yang penting dan sulit dalam matematika.
Pada Agustus 2006, Perelman dianugrahkan Fields Medal,yang dianggap luas sebagai penghargaan tertinggi yang dapat diterima bagi matematikawan. Namun dia menolak menerima penghargaan tersebut dan juga menolak hadir pada kongres tersebut.
Yup ini nama orang, nama matematikawan Rusia. Kenapa ane masukkan kedaftar ? Karena dia menolak 1 juta US Dollar atas jasanya memecahkan dugaan Poincare (kasih ke TS aja klo gk mau
). Hanya orang gila atau luar biasa jenius yang menolak uang sebesar itu. Grisha Perelman, adalah seorang matematikawan Rusia berdarah Yahudi, yang membuat kontribusi terkenal kepada Geometri Riemannian dan topologi geometri. Khususnya, dia tampaknya telah membuktikan geometrisasi konjektur Thurston. Bila demikian, ini juga menyelesaikan konjektur Poincaré yang terkenal, yang dikeluarkan pada 1904 dan dianggap sebagai masalah terbuka yang penting dan sulit dalam matematika.
Pada Agustus 2006, Perelman dianugrahkan Fields Medal,yang dianggap luas sebagai penghargaan tertinggi yang dapat diterima bagi matematikawan. Namun dia menolak menerima penghargaan tersebut dan juga menolak hadir pada kongres tersebut.
Quote:
3. Jarum Buffon
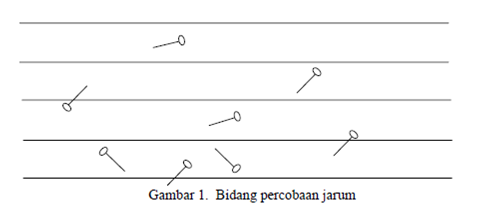
Misalkan agan berdiri di lantai dengan garis-garis paralel, yang jarak antar garisnya sama misalkan saja jarak antar garis 5 cm lalu kita menjatuhkan jarum sepanjang 5 cm, Nah pertanyaannya berapa peluang jarum tersebut jatuh diantar dua garis?
Jawabnnya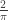
, Mmm… nilai yang mengejutkan, ya kan? 
Misalkan agan berdiri di lantai dengan garis-garis paralel, yang jarak antar garisnya sama misalkan saja jarak antar garis 5 cm lalu kita menjatuhkan jarum sepanjang 5 cm, Nah pertanyaannya berapa peluang jarum tersebut jatuh diantar dua garis?
Jawabnnya
, Mmm… nilai yang mengejutkan, ya kan? Quote:
2 . Monty Hall Problem
Masih berhubungan dengan teori peluang.
Bayangkan agan mengikuti kuis, ada tiga pintu disana sebut saja pintu 1, pintu 2 dan pintu 3., salah satu berisi mobil dan dua lainnya berisi kambing. agan disuruh memilih salah satu dari ketiga pintu dan akan mendapatkan benda di balik pintu yang agan pilih. Tentu saja agan tidak tahu di pintu berapa, mobil itu berada. Misalkan saja agan memilih pintu 1 kemudian si pembawa acara bernama monty membuka salah satu pintu bisa pintu 2 atau 3 dan ternyata berisi kambing. Lalu si Monty bertanya ke agan ” apa kamu mau mengganti pilihan?”. Nah..sekarang pertanyaan untuk ente ente semua
1. Berapa peluang agan mendapatkan mobil jika tetap memilih pintu 1?
2. Berapa peluang agan mendapatkan mobil jika mengganti pilihan?
Banyak orang termasuk para akademisi berpikiran peluangnya 1/2, mau agan menganti pilihan atau tidak tetap peluangnya 1/2. Dengan alasan mau apapun pintu yang kamu pilih tetap saja pintu tersebut hanya ada 2 kemungkinan berisi mobil atau kambing. Padahal sebenarnya peluangmu hanya 1/3 jika kamu tetap memilih pintu 1 dan peluang ente akan naik menjadi 2/3 jika kamu mengannti pilihan.(agak membingungkan sedikit ya)
Masih berhubungan dengan teori peluang.
Bayangkan agan mengikuti kuis, ada tiga pintu disana sebut saja pintu 1, pintu 2 dan pintu 3., salah satu berisi mobil dan dua lainnya berisi kambing. agan disuruh memilih salah satu dari ketiga pintu dan akan mendapatkan benda di balik pintu yang agan pilih. Tentu saja agan tidak tahu di pintu berapa, mobil itu berada. Misalkan saja agan memilih pintu 1 kemudian si pembawa acara bernama monty membuka salah satu pintu bisa pintu 2 atau 3 dan ternyata berisi kambing. Lalu si Monty bertanya ke agan ” apa kamu mau mengganti pilihan?”. Nah..sekarang pertanyaan untuk ente ente semua
1. Berapa peluang agan mendapatkan mobil jika tetap memilih pintu 1?
2. Berapa peluang agan mendapatkan mobil jika mengganti pilihan?
Banyak orang termasuk para akademisi berpikiran peluangnya 1/2, mau agan menganti pilihan atau tidak tetap peluangnya 1/2. Dengan alasan mau apapun pintu yang kamu pilih tetap saja pintu tersebut hanya ada 2 kemungkinan berisi mobil atau kambing. Padahal sebenarnya peluangmu hanya 1/3 jika kamu tetap memilih pintu 1 dan peluang ente akan naik menjadi 2/3 jika kamu mengannti pilihan.(agak membingungkan sedikit ya
)Quote:
1. Paradoks Banach Tarski
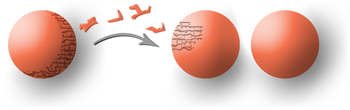
Tentu saja yang paling ajaib di matematika adalah Paradoks Banachh Tarski. Didunia matematika kita bisa memotong apel menjadi beberapa potong lalu kita bisa menyusun potongan2 tersebut menjadi 2 apel yang identik dengan apel sebelumnya.
Tentu saja yang paling ajaib di matematika adalah Paradoks Banachh Tarski. Didunia matematika kita bisa memotong apel menjadi beberapa potong lalu kita bisa menyusun potongan2 tersebut menjadi 2 apel yang identik dengan apel sebelumnya.
Spoiler for Penjelasan:
Penjelasan:
Perlu dipahami bahwa bola padat yang dimaksudkan disini adalah bola padat menurut pemahaman matematika yaitu himpunan titik-titik tak hingga yang didefinisikan sebagai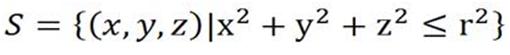
dengan r jari-jari bola.
Teori yang ditemukan oleh Stefan Banach dan Alfred Tarski ini melibatkan beberapa teori sebelumnya yaitu Translasi, rotasi, isometri, kongruen dan aksioma pilihan.
Paradox Banach-Tarski (PBT) dijelaskan dalam dua versi yaitu versi lemah dan versi kuat. Kedua versi ini memperlihatkan keanehan, dan keajaiban yang berbeda.
Versi Lemah
Proses PBT yang dijelaskan dalam versi ini mempertahankan: Bentuk, Ukuran, Kepadatan, dan Volume.
Bentuk, artinya setelah proses PBT berlangsung bola padat yang dihasilkan sama seperti bola padat sebelumnya, tidak menjadi lonjong, gepeng atau setengah bola.
Ukuran, artinya jika bola padat yang dipecah berjari-jari r, maka hasil PBT akan tetap berjari-jari r juga.
Kepadatan, artinya untuk mendapatkan dua atau lebih bola padat yang memiliki ukuran dan bentuk yang sama dari susunan pecahan sebuah bola padat, tidak dilakukan peregangan, sehingga kepadatannya tetap.
Volume, artinya tidak dilakukan penambahan material kepingan dari luar kepingan sebuah bola padat sebelumnya.
Untuk lebih jelasnya, perhatikan analogi berikut :
Secara formal, PBT Versi Lemah ini mengatakan,
Untuk sebarang bola padat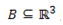
dapat dipecahkan menjadi kepingan-kepingan berhingga 
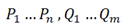dan isometri 
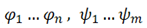pada R3 sedemikian sehingga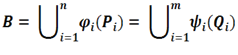 
Perlu dipahami bahwa bola padat yang dimaksudkan disini adalah bola padat menurut pemahaman matematika yaitu himpunan titik-titik tak hingga yang didefinisikan sebagai
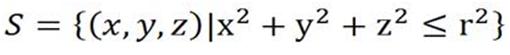
dengan r jari-jari bola.
Teori yang ditemukan oleh Stefan Banach dan Alfred Tarski ini melibatkan beberapa teori sebelumnya yaitu Translasi, rotasi, isometri, kongruen dan aksioma pilihan.
Paradox Banach-Tarski (PBT) dijelaskan dalam dua versi yaitu versi lemah dan versi kuat. Kedua versi ini memperlihatkan keanehan, dan keajaiban yang berbeda.
Versi Lemah
Proses PBT yang dijelaskan dalam versi ini mempertahankan: Bentuk, Ukuran, Kepadatan, dan Volume.
Bentuk, artinya setelah proses PBT berlangsung bola padat yang dihasilkan sama seperti bola padat sebelumnya, tidak menjadi lonjong, gepeng atau setengah bola.
Ukuran, artinya jika bola padat yang dipecah berjari-jari r, maka hasil PBT akan tetap berjari-jari r juga.
Kepadatan, artinya untuk mendapatkan dua atau lebih bola padat yang memiliki ukuran dan bentuk yang sama dari susunan pecahan sebuah bola padat, tidak dilakukan peregangan, sehingga kepadatannya tetap.
Volume, artinya tidak dilakukan penambahan material kepingan dari luar kepingan sebuah bola padat sebelumnya.
Untuk lebih jelasnya, perhatikan analogi berikut :
Secara formal, PBT Versi Lemah ini mengatakan,
Untuk sebarang bola padat
dapat dipecahkan menjadi kepingan-kepingan berhingga 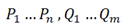dan isometri 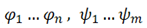pada R3 sedemikian sehingga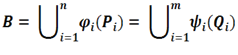
Quote:
Spoiler for Thanks For Cendol:
Thanks Semuanya yg udah ndukung n kasih cendol
semoga amal ente bermanfaat bagi orang lain
Quote:
Sebenarnya masih banyak hal-hal yang saya anggap ajaib di Matematika tapi ane taunya cuma segini ya gan mungkin ada yang tahu bisa nambahin . sekiranya cukup dulu ya (kalau perkataan ane kurang enak mohon maaf) kalau ada yang ikhlas ngasih 
ane doain masuk surga
mungkin ada yang tahu bisa nambahin . sekiranya cukup dulu ya (kalau perkataan ane kurang enak mohon maaf) kalau ada yang ikhlas ngasih ane doain masuk surgaQuote:
Polling
0 suara
(Jujur) Apkah Ente Suka Matematika ?
Diubah oleh forderation 18-09-2013 07:32
0
131.7K
2K
Tulis komentar menarik atau mention replykgpt untuk ngobrol seru
Mari bergabung, dapatkan informasi dan teman baru!
The Lounge
925.8KThread•93.2KAnggota
Urutkan
Terlama
Tulis komentar menarik atau mention replykgpt untuk ngobrol seru
